题目内容
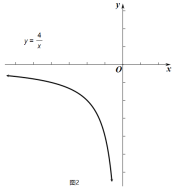
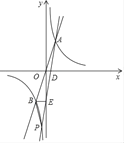
【题目】如图,过原点O的直线与双曲线y=![]() 交于上A(m,n)、B,过点A的直线交x轴正半轴于点D,交y轴负半轴于点E,交双曲线y=
交于上A(m,n)、B,过点A的直线交x轴正半轴于点D,交y轴负半轴于点E,交双曲线y=![]() 于点P.
于点P.
(1)当m=2时,求n的值;
(2)当OD:OE=1:2,且m=3时,求点P的坐标;
(3)若AD=DE,连接BE,BP,求△PBE的面积.
【答案】(1)3;(2)P(﹣2,﹣3);(3)3.
【解析】
(1)把A(2,n)代入解析式即可求出n;(2)先求出A点坐标,设OD=a,则OE=2a,得D(a,0),E(0,﹣2a),直线DE的解析式为y=2x﹣2a,把点A(3,2)代入求出a,再联立两函数即可求出交点P;(3)由AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,故A(m,n),E(0,﹣n),D(![]() m,0),求得直线DE的解析式为y=
m,0),求得直线DE的解析式为y=![]() x﹣n,又mn=6,得y=
x﹣n,又mn=6,得y=![]() x﹣n,与y=
x﹣n,与y=![]() 联立得
联立得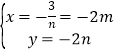 ,即为P点坐标,由直线AB的解析式为y=
,即为P点坐标,由直线AB的解析式为y=![]() x与双曲线联立解得B(﹣m,﹣n),再根据S△PBE=
x与双曲线联立解得B(﹣m,﹣n),再根据S△PBE=![]() BE×|yE﹣yP|=
BE×|yE﹣yP|=![]() ×m×|﹣n﹣(﹣2n)|求出等于3.
×m×|﹣n﹣(﹣2n)|求出等于3.
解:(1)∵点A(m,n)在双曲线y=![]() 上,
上,
∴mn=6,
∵m=2,
∴n=3;
(2)由(1)知,mn=6,
∵m=3,
∴n=2,
∴A(3,2),
∵OD:OE=1:2,
设OD=a,则OE=2a,
∵点D在x轴坐标轴上,点E在y轴负半轴上,
∴D(a,0),E(0,﹣2a),
∴直线DE的解析式为y=2x﹣2a,
∵点A(3,2)在直线y=2x﹣2a上,
∴6﹣2a=2,
∴a=2,
∴直线DE的解析式为y=2x﹣4①,
∵双曲线的解析式为y=![]() ②,
②,
联立①②解得,![]() (点A的横纵坐标,所以舍去)或
(点A的横纵坐标,所以舍去)或![]() ,
,
∴P(﹣2,﹣3);
(3)∵AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,A(m,n),
∴E(0,﹣n),D(![]() m,0),
m,0),
∴直线DE的解析式为y=![]() x﹣n,
x﹣n,
∵mn=6,
∴m=![]() ,
,
∴y=![]() x﹣n③,
x﹣n③,
∵双曲线的解析式为y=![]() ④,
④,
联立③④解得,
∴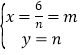 (点A的横纵坐标,所以舍去)或
(点A的横纵坐标,所以舍去)或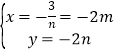 ,
,
∴P(﹣2m,﹣2n),
∵A(m,n),
∴直线AB的解析式为y=![]() x⑤.
x⑤.
联立④⑤解得,![]() (点A的横纵坐标,所以舍去)或
(点A的横纵坐标,所以舍去)或![]()
∴B(﹣m,﹣n),
∵E(0,﹣n),
∴BE∥x轴,
∴S△PBE=![]() BE×|yE﹣yP|=
BE×|yE﹣yP|=![]() ×m×|﹣n﹣(﹣2n)|=
×m×|﹣n﹣(﹣2n)|=![]() mn=3.
mn=3.

 阅读快车系列答案
阅读快车系列答案【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?