题目内容
【题目】对于自变量为![]() 的函数,当
的函数,当![]() 时,其函数值也为
时,其函数值也为![]() ,则称点
,则称点![]() 为此函数的不动点.若函数
为此函数的不动点.若函数![]() 图象上有两个不动点
图象上有两个不动点![]() 、
、![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求函数
,求函数![]() 的不动点坐标;
的不动点坐标;
(2)求证;![]() ;
;
(3)若函数![]() ,
,![]() ,
,![]() ,当
,当![]() 时,
时,
①求证:![]() ;
;
②求证:![]() .
.
【答案】(1)![]() ,
,![]() (2)证明见解析(3)①证明见解析③证明见解析
(2)证明见解析(3)①证明见解析③证明见解析
【解析】
(1)先求出函数解析式,再令y=x2+2x=x,解x即可;
(2)证明出函数的最小值,根据不动点定义即可证明;
(3)①②进行作差运算,得到二次函数,根据二次函数图象的性质进行证明即可.
(1)∵![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
令![]()
∴![]() ,即
,即![]() ,
,![]() .
.
∴![]() ,
,![]()
(2)证明:∵![]() 的顶点坐标是
的顶点坐标是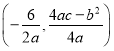
∵![]()
∴![]()
∵![]() 是不动点
是不动点
∴![]() .∴
.∴![]()
∴![]()
(3)①证明:令![]()
∵![]() 是开口向上,与
是开口向上,与![]() 轴有两个交点的二次函数
轴有两个交点的二次函数
∴当![]() 时,
时,![]() 随着
随着![]() 增大而减小
增大而减小
∴当![]() 时
时![]()
∴![]() .即
.即![]()
②证明:令![]() 的对称轴
的对称轴![]()
∴![]()
∵![]()
∴![]()
由(2)得![]()
∴![]() 即
即![]()
∴当![]() 时,
时,![]()
在![]() 时,
时,![]() 随着
随着![]() 增大而增大
增大而增大
当![]() 时
时![]()
∴![]()
当![]() 时
时
∵当![]() 时,对应
时,对应![]() 项相与当
项相与当![]() 时对应
时对应![]() 项相等.
项相等.
∴![]() 对应
对应
最大值只能由当![]() 时,求当
时,求当![]() 时取得
时取得
∴当![]() 时
时
![]() 随着
随着![]() 增大而增大
增大而增大
∴![]() 对应
对应![]() .
.
∴![]() 最大,则
最大,则![]() 最大
最大
∴![]()

 习题精选系列答案
习题精选系列答案【题目】某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求![]() 的值.
的值.
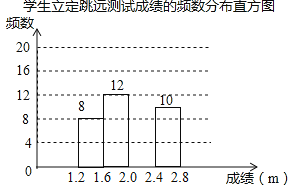
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?