题目内容
【题目】如图，正方形
的边长为2，点
在
上，四边形
也是正方形，以
为圆心，
长为半径画
，连结
，
，则图中阴影部分面积为（ ）
A.
B.
C.
D.
【答案】A
【解析】
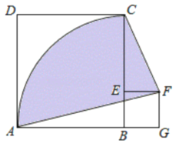
设正方形BEFG的边长为a，根据正方形的性质得出AB=BC=2，BG=FG=BE=EF=a，∠ABE=∠CEF=∠CBG=90°，根据图形得出阴影部分的面积S=S扇形ABC+S正方形BEFG+S△CEF-S△AGF，分别求出即可．
设正方形BEFG的边长为a，
∵四边形ABCD和四边形BEFG都是正方形，
∴AB=BC=2，BG=FG=BE=EF=a，∠ABE=∠CEF=∠CBG=90°，
∴阴影部分的面积S=S扇形ABC+S正方形BEFG+S△CEF-S△AGF
=
=π，
故选A．
练习册系列答案
相关题目
【题目】某经销商销售一种成本价为10元/kg的商品，已知销售价不低于成本价，且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y（kg）与售价x（元/kg）之间满足一次函数关系，对应关系如下表所示：
x | 12 | 14 | 15 | 17 |
y | 36 | 32 | 30 | 26 |
⑴求y与x之间的函数关系式，并写出自变量x的取值范围；
⑵若该经销商想使这种商品获得平均每天168元的利润，求售价应定为多少元/kg？
⑶设销售这种商品每天所获得的利润为W元，求W与x之间的函数关系式；并求出该商品销售单价定为多少元时，才能使经销商所获利润最大？最大利润是多少？
