题目内容
已知二次函数
．
（1）证明：不论
取何值,该函数图象与
轴总有两个公共点;
（2）若该函数的图象与
轴交于点(0,5),求出顶点坐标,并画出该函数图象．
（1）证明见解析;（2）顶点坐标：（
,
）,图像见解析．
解析试题分析：（1）证明对应的一元二次方程﹣x2+（m﹣3）x+m=0的根的判别式大于0,即可作出判断;
（2）把x=0,y=5代入抛物线的解析式,即可得到一个关于m的方程,从而求得m的值,得到函数的解析式,然后把解析式化成顶点式的形式,即可求解．
试题解析：（1）令
,
,
,
=
=
,
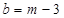∵（m-1）2≥0
∴（m-1）2+8＞0
∴b2-4ac＞0
∴不论取何值,该函数图象与轴总有两个公共点;
（2）把
,
代入
∴
∴
=
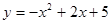顶点坐标：（,）．
函数图象：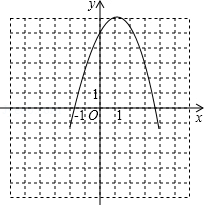
考点：二次函数的图象．
练习册系列答案
相关题目
x－4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D．设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值？最小值为多少？
（k为正整数）.
（k为正整数）有两个不相等的整数解，点A（m，y1），B（m+1，y2），C（m+2，y3）都在二次函数
轴的交点坐标.已知抛物线y=x²-4x+3．
（1）该抛物线的对称轴是 ，顶点坐标 ；
（2）将该抛物线向上平移2个单位长度，再向左平移3个单位长度得到新的二次函数图像，请写出相应的解析式，并用列表，描点，连线的方法画出新二次函数的图像；
| x | … | | | | | | … |
| y | … | | | | | | … |
（3）新图像上两点A（x1，y1），B（x2，y2），它们的横坐标满足＜-2，且-1＜＜0，试比较y1，y2，0三者的大小关系．
，自变量的取值范围是 ；
与y轴交于点C（0，4），与x轴交于点A、B，点A的坐标为（4，0）.
与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）.问：是否存在这样的直线