��Ŀ����
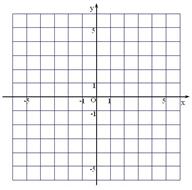
��֪����ͼ�������� ��y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.
��y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.
��1����������ߵĽ���ʽ��
��2����Q���߶�AB�ϵĶ��㣬����Q��QE��AC����BC�ڵ�E������CQ.����CQE��������ʱ�����Q�����ꣻ
��3����ƽ����x��Ķ�ֱ�� ��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ��
��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ�� ��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵������.
��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵������.
��1��y=��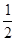
 ����2��Q��1��0������3�����ڣ�P1��
����2��Q��1��0������3�����ڣ�P1��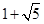 ��2����P2��
��2����P2��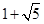 ��2����P3��
��2����P3�� ��3����P4��
��3����P4�� ��3��.
��3��.
���������������1���ѵ�A�͵�C��������� �����ô���ϵ�������������ĸa��c��ֵ���Ӷ����������ϵʽ����2�����Q������Ϊ��m��0��������EQ��AC���õ���BQE�ס�BAC���������������ζ�Ӧ�ߵıȵ������Ʊȣ�����ĸm��ʾ��BG�ij���Ȼ�����
�����ô���ϵ�������������ĸa��c��ֵ���Ӷ����������ϵʽ����2�����Q������Ϊ��m��0��������EQ��AC���õ���BQE�ס�BAC���������������ζ�Ӧ�ߵıȵ������Ʊȣ�����ĸm��ʾ��BG�ij���Ȼ�����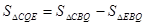 ��ʾ����CQE����ǹ�����ĸm�Ķ��κ��������ݶ��κ��������ʼ������������ֵ����3���������⣬������������Ȼ���ͼ�Σ�Ȼ����ݵ��������ε����ʽ��.
��ʾ����CQE����ǹ�����ĸm�Ķ��κ��������ݶ��κ��������ʼ������������ֵ����3���������⣬������������Ȼ���ͼ�Σ�Ȼ����ݵ��������ε����ʽ��.
�����������1��������� ��
��
���
�����������ߵý���ʽΪ��y=��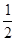
 .
.
��2�����Q��������m��0��������E��EG��X�����G
�ɣ�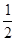
 =0����
=0����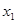 =��2��
=��2��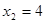 .
.
���B����������2��0��.
��AB=6��BQ= m��2.
�֡�QE��AC��
���BQE�ס�BAC��
�� .
.
��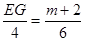 .
.
��EG=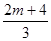 .
.
��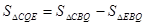
=
=
=
=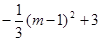 .
.
�֡ߣ�2��m��4��
�൱m=1ʱ��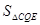 �����ֵΪ3����ʱQ��1��0��.
�����ֵΪ3����ʱQ��1��0��.
��3������.�ڡ�ODF��
����DO=DFʱ��
��A��4��0����D��2��0����
��AD=OD=DF=2.
����RT��AOC��OA=OC=4��
���OAC=45��.
���DFA=��OAC=45��.
���ADF=90��.
��ʱ��F������Ϊ(2��2).
��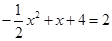 ��x1��
��x1��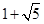 ��x2��
��x2�� .
.
��ʱ��P������Ϊ:P��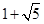 ��2����P��
��2����P��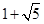 ��2��.
��2��.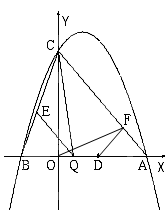
����OF��DFʱ������F��FM��x�����M��
�ɵ��������ε����ʵ�:OM�� OD��1.
OD��1.
��F��1��3��.
����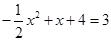 ��x1��
��x1�� ��x2��
��x2�� .
.
��ʱ��P������Ϊ:P�� ��3����P��
��3����P�� ��3��.
��3��.
����OD��OF��
��OA��OC��4���ҡ�AOC��90�㣬
��AC�� .
.
���O��AC�ľ���Ϊ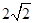 .
.
��OF��OD��2��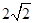 ����OF��
����OF��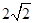 ì�ܣ�
ì�ܣ�
��AC�ϲ����ڵ�ʹ��OF��OD��2.
��ʱ����������ֱ��L��ʹ�á�ODF�ǵ���������.
��������������������ֱ��L��ʹ�á�ODF�ǵ���������.
�����P������Ϊ:
P1��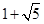 ��2����P2��
��2����P2��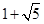 ��2����P3��
��2����P3�� ��3����P4��
��3����P4�� ��3��.
��3��.
���㣺1����ϵ��������κ����Ĺ�ϵʽ��2���κ�����ͼ����������Ӧ�ã����������ε����ʣ�3��������.

 ��
��
 ȡ��ֵ,�ú���ͼ����
ȡ��ֵ,�ú���ͼ���� ����������������;
����������������; �ύ�ڵ�(0,5),�����������,�������ú���ͼ��
�ύ�ڵ�(0,5),�����������,�������ú���ͼ��
 �����㻯��
�����㻯�� ����ʽ������ֱ������ϵ�л���
����ʽ������ֱ������ϵ�л��� ��
�� �ǣ�1����ͼ���ϵ����㣬��
�ǣ�1����ͼ���ϵ����㣬�� ����ֱ��д��
����ֱ��д�� ��
�� �Ĵ�С��ϵ��
�Ĵ�С��ϵ�� �ĸ�����Ҫ������ͼ�ۼ���˵�������
�ĸ�����Ҫ������ͼ�ۼ���˵�������
 x2��10������BD��
x2��10������BD�� CD.
CD.


 ��ֱ��
��ֱ�� ����C��D���㣬���е�C��y���ϣ���D������Ϊ
����C��D���㣬���е�C��y���ϣ���D������Ϊ ����P��y���Ҳ����������һ���㣬����P��
����P��y���Ҳ����������һ���㣬����P�� ���ڵ�E����CD�ڵ�F.
���ڵ�E����CD�ڵ�F.
 ����ֱ��д����Ӧ�ĵ�P������
����ֱ��д����Ӧ�ĵ�P������