题目内容
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长等于_____;
(Ⅱ)在线段AC上有一点D,满足AB2=ADAC,请在如图所示的网格中,用无刻度的直尺,画出点D,并简要说明点D的位置是如何找到的(不要求证明)_____.
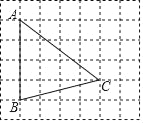
【答案】5 见解析.
【解析】
(1)由勾股定理即可求解;(2)寻找格点M和N,构建与△ABC全等的△AMN,易证MN⊥AC,从而得到MN与AC的交点即为所求D点.
(1)AC=![]() ;
;
(2)如图,连接格点M和N,由图可知:
AB=AM=4,
BC=AN=![]() ,
,
AC=MN=![]() ,
,
∴△ABC≌△MAN,
∴∠AMN=∠BAC,
∴∠MAD+∠CAB=∠MAD+∠AMN=90°,
∴MN⊥AC,
易解得△MAN以MN为底时的高为![]() ,
,
∵AB2=ADAC,
∴AD=AB2÷AC=![]() ,
,
综上可知,MN与AC的交点即为所求D点.

练习册系列答案
相关题目





