Question

【题目】在平面直角坐标系中，存在抛物线以及两点．

(1)求该抛物线的顶点坐标；(用含的代数式表示)

(2)若该抛物线经过点，求此抛物线的表达式；

(3)若该抛物线与线段有公共点，结合图象，求的取值范围．

Answer 1

【答案】（1）；（2）：或；（3）或.

【解析】

（1）根据题意将抛物线的一般解析式化为顶点式即可得出抛物线的顶点坐标；

（2）根据题意将代入求出m的值即可求得该抛物线的表达式；

（3）根据题意分m≥0，m＜0两种情形，分别构建不等式解决问题即可．

解：（1）∵抛物线解析式为：，

∴顶点坐标为：.

（2）∵抛物线经过点，

∴，解得，

所以该抛物线的表达式为：或.

（3）当m≥0时，如图1中，

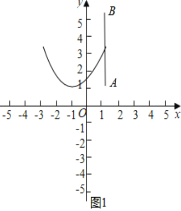
观察图象可知：，

∴且，

解得．

当m＜0时，如图2中，

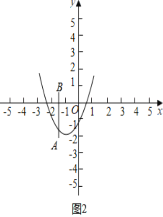
观察图象可知：，

∴m2+2m≥0且m2+2m-2≤0，

解得，

综上所述，满足条件的m的值为：或．