题目内容
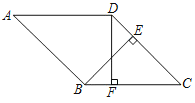
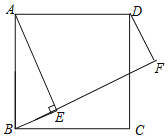
【题目】如图,点E是正方形ABCD内一动点,满足∠AEB=90°且∠BAE<45°,过点D作DF⊥BE交BE的延长线于点F.
(1)依题意补全图形;
(2)用等式表示线段EF,DF,BE之间的数量关系,并证明;
(3)连接CE,若AB=2![]() ,请直接写出线段CE长度的最小值.
,请直接写出线段CE长度的最小值.

【答案】(1)见解析;(2)EF=DF+BE,证明见解析;(3)CE的最小值为![]() .
.
【解析】
(1)依题意补全图形;
(2)过点A作AM⊥FD交FD的延长线于点M,可证四边形AEFM是矩形,由“AAS”可证△AEB≌△AMD,可得BE=DM,AE=AM,可证矩形AEFM是正方形,可得EF=MF,可得结论;
(3)取AB中点O,连接OC,由勾股定理可求OC=5,由点E在以O为圆心,OB为半径的圆上,可得当点E在OC上时,CE有最小值,即可求解.
解:(1)依题意补全图形,如图,
(2)线段EF,DF,BE的数量关系为:EF=DF+BE,
理由如下:如图,过点A作AM⊥FD交FD的延长线于点M,
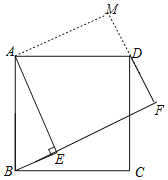
∵∠M=∠F=∠AEF=90°,
∴四边形AEFM是矩形,
∴∠DAE+∠MAD=90°,
∵四边形ABCD是正方形,
∴∠BAE+∠DAE=90°,AB=AD,
∴∠BAE=∠MAD.
又∵∠AEB=∠M=90°,
∴△AEB≌△AMD(AAS)
∴BE=DM,AE=AM,
∴矩形AEFM是正方形,
∴EF=MF,
∵MF=DF+DM,
∴EF=DF+BE;
(3)如图,取AB中点O,连接OC,
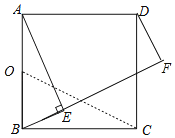
∵AB=2![]()
∴OB=![]() ,
,
∴OC=![]() =5,
=5,
∵∠AEB=90°,
∴点E在以O为圆心,OB为半径的圆上,
∴当点E在OC上时,CE有最小值,
∴CE的最小值为![]() .
.

练习册系列答案
相关题目