Question

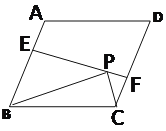
【题目】如图,在菱形ABCD中，sinD=,E、F分别是AB,CD上的点，BC=5，AE=CF=2，点P是线段EF上一点，则当△BPC时直角三角形时，CP的长为____________

Answer 1

【答案】4或或

【解析】根据∠D的正弦求出以AD为斜边的直角三角形的两直角边分别为3、4，然后以DC所在的直线为x轴，点F为坐标原点建立平面直角坐标系，根据菱形的对角线互相垂直平方可知点P为菱形的对角线的交点时∠BPC=90°，点P与点E重合时∠BPC=90°；∠BCP=90°时写出点B、C的坐标，利用待定系数法求一次函数解析式求出直线OE、BC的解析式，再求出CP的解析式，然后联立直线OE、CP的解析式求出点P的坐标，再利用勾股定理列式计算即可求出CP．

∵sin∠D=，菱形边AD=BC=5，

∴以AD为斜边的直角三角形的两直角边分别为3、4

如图，以DC所在的直线为x轴，点F为坐标原点建立平面直角坐标系，

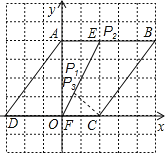
∵菱形ABCD的对角线AC⊥BD，

∴点P为菱形的对角线的交点时∠BPC=90°，

此时，CP=AC=×，

点P与点E重合时∠BPC=90°，

此时，CP=4；

∠BCP=90°时，由图可知，点B（5，4）、C（2，0），

易求直线OE的解析式为y=2x，

设直线BC的解析式为y=kx+b，

则，

解得，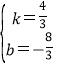

所以，直线BC的解析式为y=x-，

∵CP⊥BC，

∴设直线CP的解析式为y=-x+c，

将点C（2，0）代入得，-×2+c=0，

解得c=，

所以，直线CP的解析式为y=-x+，

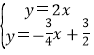联立，解得，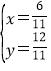

所以，点P的坐标为（，），

此时，CP=，

综上所述，当△BPC是直角三角形时，CP的长为或4或．

故答案为：或4或．