题目内容
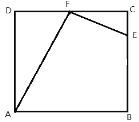
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
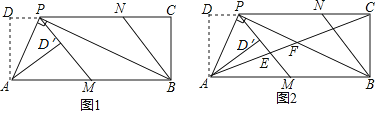
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
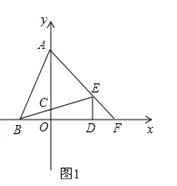
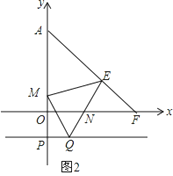
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)四边形PMBN是菱形,理由见解析;(3)![]()
【解析】(1)过点P作PG⊥AB于点G,易知四边形DPGA,四边形PCBG是矩形,所以AD=PG,DP=AG,GB=PC,易证△APG∽△PBG,所以PG2=AGGB,即AD2=DPPC;
(2)DP∥AB,所以∠DPA=∠PAM,由题意可知:∠DPA=∠APM,所以∠PAM=∠APM,由于∠APB-∠PAM=∠APB-∠APM,即∠ABP=∠MPB,从而可知PM=MB=AM,又易证四边形PMBN是平行四边形,所以四边形PMBN是菱形;
(3)由于![]() ,可设DP=k,AD=2k,由(1)可知:AG=DP=k,PG=AD=2k,从而求出GB=PC=4k,AB=AG+GB=5k,由于CP∥AB,从而可证△PCF∽△BAF,△PCE∽△MAE,从而可得
,可设DP=k,AD=2k,由(1)可知:AG=DP=k,PG=AD=2k,从而求出GB=PC=4k,AB=AG+GB=5k,由于CP∥AB,从而可证△PCF∽△BAF,△PCE∽△MAE,从而可得![]() ,
,![]() ,从而可求出EF=AF-AE=
,从而可求出EF=AF-AE=![]() AC-
AC-![]() AC=
AC=![]() AC,从而可得
AC,从而可得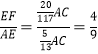 .
.
(1)过点P作PG⊥AB于点G,
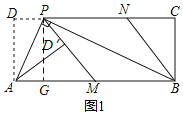
∴易知四边形DPGA,四边形PCBG是矩形,
∴AD=PG,DP=AG,GB=PC
∵∠APB=90°,
∴∠APG+∠GPB=∠GPB+∠PBG=90°,
∴∠APG=∠PBG,
∴△APG∽△PBG,
∴![]() ,
,
∴PG2=AGGB,
即AD2=DPPC;
(2)∵DP∥AB,
∴∠DPA=∠PAM,
由题意可知:∠DPA=∠APM,
∴∠PAM=∠APM,
∵∠APB-∠PAM=∠APB-∠APM,
即∠ABP=∠MPB
∴AM=PM,PM=MB,
∴PM=MB,
又易证四边形PMBN是平行四边形,
∴四边形PMBN是菱形;
(3)由于![]() ,
,
可设DP=k,AD=2k,
由(1)可知:AG=DP=k,PG=AD=2k,
∵PG2=AGGB,
∴4k2=kGB,
∴GB=PC=4k,
AB=AG+GB=5k,
∵CP∥AB,
∴△PCF∽△BAF,
∴![]() ,
,
∴![]() ,
,
又易证:△PCE∽△MAE,AM=![]() AB=
AB=![]() ,
,
∴![]()
∴![]() ,
,
∴EF=AF-AE=![]() AC-
AC-![]() AC=
AC=![]() AC,
AC,
∴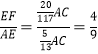 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案