Question

【题目】△ABC为等边三角形，在平面内找一点P，使△PAB，△PBC，△PAC均为等腰三角形，则这样的点P的个数为_____．

Answer 1

【答案】10个

【解析】

点P在三角形内部时，点P是边AB、BC、CA的垂直平分线的交点，是三角形的外心，点P在三角形外部时，根据线段垂直平分线的性质可得分别以三角形各顶点为圆心，边长为半径，交垂直平分线的交点就是满足要求的．

如图，

点P在等边△ABC内时，

∵△PBC、△PAB、△PAC均为等腰三角形，

∴P点为等边△ABC的外心；

当点P在三角形外部时，

∵线段垂直平分线上的点到线段两端点的距离相等，

∴分别以三角形各顶点为圆心，边长为半径，与各边垂直平分线的交点即是满足要求的点．

每条垂直平分线上得3个交点，再加三角形的外心，一共10个，

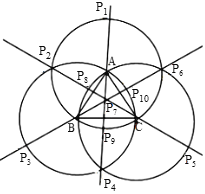
故答案为：10个