题目内容
【题目】某校计划建一间多功能数学实验室,将采购两类桌椅:A类是三角形桌,每桌可坐3人,B类是五边形桌,每桌可坐5人.学校拟选择甲、乙两家公司中的一家来采购,两家公司的标价均相同,且规定两类桌椅均只能在同一家公司采购.甲公司对两类桌椅均是以标价出售;乙公司对A类桌椅涨价20%、B类桌椅降价20%出售.经咨询,两家公司给出的数量和费用如下表:
A类桌椅(套) | B类桌椅(套) | 总费用(元) | |
甲公司 | 6 | 5 | 1900 |
乙公司 | 3 | 7 | 1660 |
(1)求第一次购买时,A、B两类桌椅每套的价格分别是多少?
(2)如果该数学实验室需设置48个座位,学校到甲公司采购,应分别采购A、B两类桌椅各多少套时所需费用最少?
【答案】(1)A、B两类桌椅每套的价格分别是150元、200元;(2)应分别采购A、B两类桌椅分别1套、9套时所需费用最少
【解析】
(1)根据题意和表格中的数据可以列出相应的方程组,从而可以解答本题;
(2)根据题意可以得到相应的不等式,然后根据不等式的性质和一次函数的性质即可解答本题,注意3x+5y=48.
(1)设A、B两类桌椅每套的价格分别是a元、b元,
![]() ,
,
解得,![]() ,
,
答:A、B两类桌椅每套的价格分别是150元、200元;
(2)设到甲公司采购A类桌椅x套,B类桌椅y套,所需费用为w元,
w=150x+200y=50(3x+4y),
∵3x+5y=48,
∴3x=48﹣5y,
∴w=50(48﹣5y+4y)=50(48﹣y)=﹣50y+2400,
∴w随y的增大而减小,
∵3x+5y=48,
∴y的最大值是9,此时x=1,
∴当y=9时,w取得最小值,此时w=1950,
答:应分别采购A、B两类桌椅分别1套、9套时所需费用最少.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
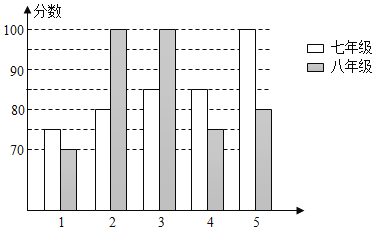
(1)根据所给信息填写表格;
平均数(分) | 中位数(分) | 众数(分) | |
七年级 | 85 | ||
八年级 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.