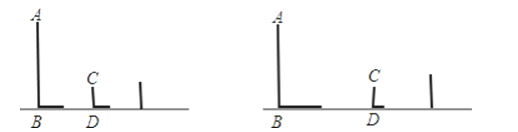题目内容
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
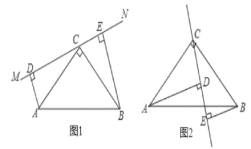
(1)当直线MN绕点C旋转到图1的位置时,△ADC和△CEB全等吗?请说明理由;
(2)聪明的小亮发现,当直线MN绕点C旋转到图1的位置时,可得DE=AD+BE,请你说明其中的理由;
(3)小亮将直线MN绕点C旋转到图2的位置,发现DE、AD、BE之间存在着一个新的数量关系,请直接写出这一数量关系。
【答案】(1)全等,理由见解析;(2)见解析;(3)DE=ADBE.理由见解析
【解析】
(1)根据同角的余角相等得到∠ACD=∠BCE,证明△ADC≌△CEB即可;
(2)根据全等三角形的性质得到BE=CD,CE=AD,结合图形得到结论;
(3)与(1)的证明方法类似,证明△ADC≌△CEB即可.
(1)△ADC≌△CEB.
理由如下:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵BE⊥MN,
∴∠CBE+∠BCE=90°,
∴∠ACD=∠BCE,
在△ADC和△CEB中,
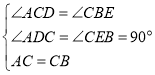 ,
,
∴△ADC≌△CEB;
(2)∵△ADC≌△CEB,
∴BE=CD,CE=AD,
∴DE=CE+CD=AD+BE;
(3)DE=ADBE.
证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥MN,
∴∠ACD+∠DAC=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
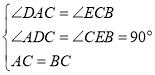 ,
,
∴△ADC≌△CEB,
∴AD=CE,CD=BE,
∴DE=CECD=ADBE.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】某校计划建一间多功能数学实验室,将采购两类桌椅:A类是三角形桌,每桌可坐3人,B类是五边形桌,每桌可坐5人.学校拟选择甲、乙两家公司中的一家来采购,两家公司的标价均相同,且规定两类桌椅均只能在同一家公司采购.甲公司对两类桌椅均是以标价出售;乙公司对A类桌椅涨价20%、B类桌椅降价20%出售.经咨询,两家公司给出的数量和费用如下表:
A类桌椅(套) | B类桌椅(套) | 总费用(元) | |
甲公司 | 6 | 5 | 1900 |
乙公司 | 3 | 7 | 1660 |
(1)求第一次购买时,A、B两类桌椅每套的价格分别是多少?
(2)如果该数学实验室需设置48个座位,学校到甲公司采购,应分别采购A、B两类桌椅各多少套时所需费用最少?