题目内容
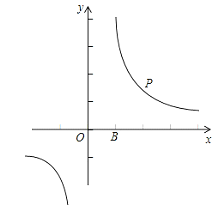
【题目】如图,Rt△ABC中,∠C=90°,AC=2,BC=1,以斜边为一边向右上方作正方形ABDE,连接CD,则CD的长为_____.
【答案】![]()
【解析】
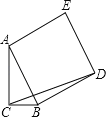
过D作DG⊥CB交CB的延长线于G,根据正方形的性质得到AB=BD,∠ABD=90°,根据余角的性质得到∠CAB=∠DBG,根据全等三角形的性质得到BG=AC=2,DG=BC=1,根据勾股定理即可得到结论.
如图所示:过D作DG⊥CB交CB的延长线于G,
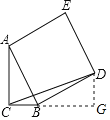
∵四边形ABDE是正方形,
∴AB=BD,∠ABD=90°,
∵∠ACB=∠DGB=90°,
∴∠ABC+∠BAC=∠ABC+∠DBG=90°,
∴∠CAB=∠DBG,
在△ABC和△BDG中
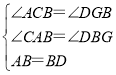 ,
,
∴△ABC≌△BDG(AAS),
∴BG=AC=2,DG=BC=1,
∴CD=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】某校计划建一间多功能数学实验室,将采购两类桌椅:A类是三角形桌,每桌可坐3人,B类是五边形桌,每桌可坐5人.学校拟选择甲、乙两家公司中的一家来采购,两家公司的标价均相同,且规定两类桌椅均只能在同一家公司采购.甲公司对两类桌椅均是以标价出售;乙公司对A类桌椅涨价20%、B类桌椅降价20%出售.经咨询,两家公司给出的数量和费用如下表:
A类桌椅(套) | B类桌椅(套) | 总费用(元) | |
甲公司 | 6 | 5 | 1900 |
乙公司 | 3 | 7 | 1660 |
(1)求第一次购买时,A、B两类桌椅每套的价格分别是多少?
(2)如果该数学实验室需设置48个座位,学校到甲公司采购,应分别采购A、B两类桌椅各多少套时所需费用最少?