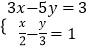题目内容
【题目】如图,先填空后证明. 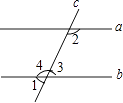
已知:∠1+∠2=180°,求证:a∥b.
证明:∵∠1=∠3 ,
∠1+∠2=180°
∴∠3+∠2=180
∴a∥b
请你再写出另一种证明方法.
【答案】对顶角相等;已知;等量代换;同旁内角互补,两直线平行
【解析】证明:∵∠1=∠3 对顶角相等, ∠1+∠2=180° 已知,
∴∠3+∠2=180° 等量代换,
∴a∥b 同旁内角互补,两直线平行.
所以答案是:对顶角相等;已知;等量代换;同旁内角互补,两直线平行.
另一种证法:
∵∠1+∠2=180°,∠1+∠4=180°,
∴∠2=∠4,
∴a∥b.
【考点精析】认真审题,首先需要了解平行线的判定(同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行).

练习册系列答案
相关题目