题目内容
【题目】
如图,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 。
。
(1)求这两个函数的表达式;
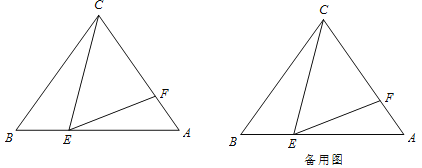
(2)如图1,若![]() ,且其两边分别与两坐标轴的正半轴交于点
,且其两边分别与两坐标轴的正半轴交于点![]() 、点
、点![]() 。求四边形
。求四边形![]() 的面积;
的面积;
(3)如图2,点![]() 是反比例函数
是反比例函数![]() 图象上的一点,过点
图象上的一点,过点![]() 作x轴、
作x轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() ,过
,过![]() 作x轴的垂线,垂足为
作x轴的垂线,垂足为![]() 。设
。设![]() 点的横坐标为
点的横坐标为![]() ,当
,当![]() 时,是否存在点
时,是否存在点![]() ,使得四边形
,使得四边形![]() 为正方形?若存在,求出
为正方形?若存在,求出![]() 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。

【答案】(1)这两个函数的表达式分别为:y=x,![]() ;(2)四边形
;(2)四边形![]() 的面积为6;(3)P点坐标为(
的面积为6;(3)P点坐标为(![]() ,
,![]() )
)
【解析】试题分析:(1)将点M(![]() ,
,![]() )分别带入
)分别带入![]() 与
与![]() 求得a、k的值,即可得这两个函数的表达式;(2)过点M分别做x轴、y轴的垂线,垂足分别为C、D,易证△AMC≌△BMD,S四边形OCMD=S四边形OAMB即可求解;(3)设P点坐标为(
求得a、k的值,即可得这两个函数的表达式;(2)过点M分别做x轴、y轴的垂线,垂足分别为C、D,易证△AMC≌△BMD,S四边形OCMD=S四边形OAMB即可求解;(3)设P点坐标为(![]() ),则PE=HG=GE=
),则PE=HG=GE=![]() ,OE=2x,再由∠MOE=45°,可得OG=GH=
,OE=2x,再由∠MOE=45°,可得OG=GH=![]() , 即可得OE= OG+GH=
, 即可得OE= OG+GH=![]() ,根据正方形的性质可得2x=
,根据正方形的性质可得2x=![]() ,解得x的值,即可求得点P的坐标.
,解得x的值,即可求得点P的坐标.
试题解析:
(1)将点M(![]() ,
,![]() )分别带入
)分别带入![]() 与
与![]() 得:
得:
![]() =a
=a![]() ,
,![]()
解得:a=1,k=6
∴这两个函数的表达式分别为:y=x,![]()
(2)过点M分别做x轴、y轴的垂线,垂足分别为C、D.
则∠MCA=∠MDB=90°,∠AMC=∠BMD=90°-∠AMD,MC=MD=![]() ,
,
∴△AMC≌△BMD,
∴S四边形OCMD=S四边形OMB=6;
(3)设P点坐标为(![]() ),则PE=HG=GE=
),则PE=HG=GE=![]() ,OE=2x,
,OE=2x,
∵∠MOE=45°,∴OG=GH=![]() , ∴OE= OG+GH=
, ∴OE= OG+GH=![]()
∴2x=![]()
![]()
∴P点坐标为(![]() ,
,![]() ).
).

 名校课堂系列答案
名校课堂系列答案【题目】嘉兴教育学院大学生小王利用暑假开展了30天的社会实践活动,参与了嘉兴浙北超市的经营,了解到某成本为15元/件的商品在x天销售的相关信息,如表表示:
销售量p(件) | P=45﹣x |
销售单价q(元/件) | 当1≤x≤18时,q=20+x 当18<x≤30时,q=38 |
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?