题目内容
如图,平面直角坐标系中有一直角梯形OMNH,点H的坐标为(-8,0),点N的坐标为(-6,-4).(1)画出直角梯形OMNH绕点O旋转180°的图形OABC,并写出顶点A,B,C的坐标(点M的对应点为A,点N的对应点为B,点H的对应点为C);
(2)求出过A,B,C三点的抛物线的表达式;
(3)截取CE=OF=AD=m,且E,F,D分别在线段CO,OA,AB上,求四边形BEFD的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFD是否存在邻边相等的情况?若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.
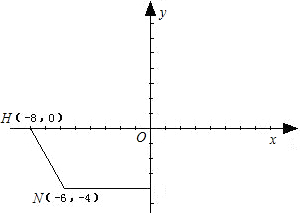
分析:(1)利用点关于中心对称性质,画出梯形OABC,分别求出各点的坐标.
(2)因为已知A,B,C三点的坐标,所以可用待定系数法求出过此三点抛物线的解析式;
(3)根据梯形及三角形的面积公式可求出四边形BEFD的面积S与m之间的函数关系式,因为在梯形AOBE中,OA最短为4,故m的取值范围为0<m<4.根据S与m之间的关系式可知当m=4时,S取最小值.又因为m=4时,原函数是无意义,故不存在m值,使S取得最小值.
(4)此题应分四种情况讨论:①BE=FE,②FD=DB,③DB=BE,④FE=FD.
(2)因为已知A,B,C三点的坐标,所以可用待定系数法求出过此三点抛物线的解析式;
(3)根据梯形及三角形的面积公式可求出四边形BEFD的面积S与m之间的函数关系式,因为在梯形AOBE中,OA最短为4,故m的取值范围为0<m<4.根据S与m之间的关系式可知当m=4时,S取最小值.又因为m=4时,原函数是无意义,故不存在m值,使S取得最小值.
(4)此题应分四种情况讨论:①BE=FE,②FD=DB,③DB=BE,④FE=FD.
解答: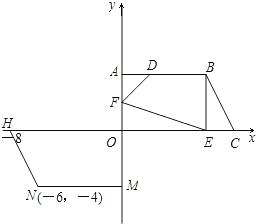 解:(1)利用中心对称性质,画出梯形OABC.(1分)
解:(1)利用中心对称性质,画出梯形OABC.(1分)
∵A,B,C三点与M,N,H分别关于点O中心对称,
∴A(0,4),B(6,4),C(8,0)(3分)
(写错一个点的坐标扣1分).
(2)设过A,B,C三点的抛物线关系式为y=ax2+bx+c,
∵抛物线过点A(0,4),
∴c=4.则抛物线关系式为
y=ax2+bx+4.(4分)
将B(6,4),C(8,0)两点坐标代入关系式,
得
(5分)
解得
(6分)
所求抛物线关系式为:y=-
x2+
x+4.(7分)
(3)∵OA=4,OC=8,
∴AF=4-m,OE=8-m.(8分)
∴S四边形EFDB=S梯形ABCO-S△ADF-S△EOF-S△BEC
=
OA(AB+OC)-
AF•AD-
OE•OF-
CE•OA
=
×4×(6+8)-
m(4-m)-
m(8-m)-
×4m
=m2-8m+28(0<m<4)(10分)
∵S=(m-4)2+12.
∴当m=4时,S的取最小值.
又∵0<m<4,
∴不存在m值,使S的取得最小值.(12分)
(4)①BE=FE,显然不成立;
②FD=DB;根据勾股定理列方程得(4-m)2+m2=(6-m)2,
解得m=-2+2
或m=-2-2
(负值舍去).
③DB=BE;且BE⊥CO时,因为BE=4,则DB=4,m=AB-DB=6-4=2.
④FE=FD;
根据勾股定理列方程得(4-m)2+m2=(6+m)2,
整理得m2-8m-20=0,m=-2或m=10,
经检验均不合题意.
∴当m=-2+2
时,DB=DF,当m=2时,BE=BD.(14分)
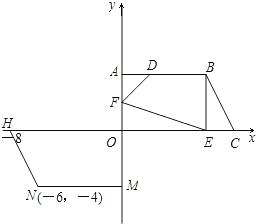 解:(1)利用中心对称性质,画出梯形OABC.(1分)
解:(1)利用中心对称性质,画出梯形OABC.(1分)∵A,B,C三点与M,N,H分别关于点O中心对称,
∴A(0,4),B(6,4),C(8,0)(3分)
(写错一个点的坐标扣1分).
(2)设过A,B,C三点的抛物线关系式为y=ax2+bx+c,
∵抛物线过点A(0,4),
∴c=4.则抛物线关系式为
y=ax2+bx+4.(4分)
将B(6,4),C(8,0)两点坐标代入关系式,
得
|
解得
|
所求抛物线关系式为:y=-
| 1 |
| 4 |
| 3 |
| 2 |
(3)∵OA=4,OC=8,
∴AF=4-m,OE=8-m.(8分)
∴S四边形EFDB=S梯形ABCO-S△ADF-S△EOF-S△BEC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=m2-8m+28(0<m<4)(10分)
∵S=(m-4)2+12.
∴当m=4时,S的取最小值.
又∵0<m<4,
∴不存在m值,使S的取得最小值.(12分)
(4)①BE=FE,显然不成立;
②FD=DB;根据勾股定理列方程得(4-m)2+m2=(6-m)2,
解得m=-2+2
| 6 |
| 6 |
③DB=BE;且BE⊥CO时,因为BE=4,则DB=4,m=AB-DB=6-4=2.
④FE=FD;
根据勾股定理列方程得(4-m)2+m2=(6+m)2,
整理得m2-8m-20=0,m=-2或m=10,
经检验均不合题意.
∴当m=-2+2
| 6 |
点评:本题结合梯形的性质考查二次函数的综合应用,注意某个图形无法解答时,常常放到其他图形中,利用图形间的“和差“关系求解.要充分利用图形特点,为解题提供思路.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.