题目内容
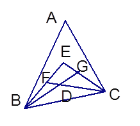
【题目】如图,在△ABC中, ∠ABC, ∠ACB的三等分线交于E, D ,若∠BFC=132°,∠BGC=128°, 则∠A=_________
【答案】80°
【解析】
由三角形内角和及角平分线的定义可得到关于∠DBC和∠DCB的方程组,可求得∠DBC+∠DCB,则可求得∠ABC+∠ACB,再利用三角形内角和可求得∠A.
解:∵∠ABC、∠ACB的三等分线交于点E、D,
∴∠FBC=2∠DBC,∠GCB=2∠DCB,
∵∠BFC=132°,∠BGC=128°,
∴∠FBC+∠DCB=180°∠BFC=180°132°=48°,
∠DBC+∠GCB=180°∠BGC=180°128°=52°,
即
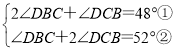 ,
,
由①+②可得:3(∠DBC+∠DCB)=100°,
∴∠ABC+∠ACB=3(∠DBC+∠DCB)=100°,
∴∠A=180°(∠ABC+∠ACB)=180°100°=80°,
故答案为80°.

练习册系列答案
相关题目