题目内容
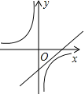
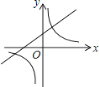
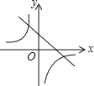
【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )

A.  B.
B. 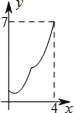 C.
C.  D.
D. 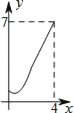
【答案】B
【解析】试题分析:分三种情况:(1)当0≤x≤![]() 时,(2)当
时,(2)当![]() <x≤2时,(3)当2<x≤4时,根据勾股定理列出函数解析式,判断其图象即可求出结果.
<x≤2时,(3)当2<x≤4时,根据勾股定理列出函数解析式,判断其图象即可求出结果.
解:(1)当0≤x≤![]() 时,
时,
如图1,过M作ME⊥BC与E,
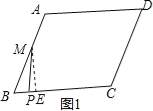
∵M为AB的中点,AB=2,
∴BM=1,
∵∠B=60°,
∴BE=![]() ,ME=
,ME=![]() ,PE=
,PE=![]() ﹣x,
﹣x,
在Rt△BME中,由勾股定理得:MP2=ME2+PE2,
∴y=![]()
![]() =x2﹣x+1;
=x2﹣x+1;
(2)当![]() <x≤2时,
<x≤2时,
如图2,过M作ME⊥BC与E,
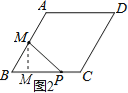
由(1)知BM=1,∠B=60°,
∴BE=![]() ,ME=
,ME=![]() ,PE=x﹣
,PE=x﹣![]() ,
,
∴MP2=ME2+PE2,
∴y=![]()
![]() =x2﹣x+1;
=x2﹣x+1;
(3)当2<x≤4时,
如图3,连结MC,
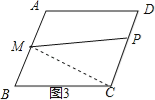
∵BM=1,BC=AB=2,∠B=60°,
∴∠BMC=90°,MC=![]() =
=![]() ,
,
∵AB∥DC,
∴∠MCD=∠BMC=90°,
∴MP2=MC2+PC2,
∴y=![]() =x2﹣4x+7;综合(1)(2)(3),只有B选项符合题意.
=x2﹣4x+7;综合(1)(2)(3),只有B选项符合题意.
故选B.

练习册系列答案
相关题目