Question

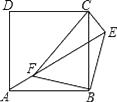
【题目】如图，⊙O是以AB为直径的圆，C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点F，连结CA，CB．
（1）求证：AC平分∠DAB；
（2）若⊙O的半径为5，且tan∠DAC= ，求BC的长．

Answer 1

【答案】
（1）证明：∵EF为切线，

∴OC⊥EF，

∵AE⊥EF，

∴AE∥OC，

∴∠EAC=∠OCA，

∵OA=OC，

∴∠OCA=∠OAC，

∴∠OAC=∠OCA，

∴AC平分∠DAB；

（2）解：∵∠OAC=∠OCA，

∴tan∠OAC=tan∠DAC= ，

设BC=x，则AC=2x，

∴AB= x，

∴ x=10，解得x=2 ，

∴BC=2 ．

【解析】（1）利用切线的性质得到OC⊥EF，而AE⊥EF，则可判定AE∥OC，利用平行线的性质得到∠EAC=∠OCA，加上∠OCA=∠OAC，于是得到∠OAC=∠OCA；（2）利用∠OAC=∠OCA得到tan∠OAC=tan∠DAC= ，设BC=x，则AC=2x，根据勾股定理得到AB= x，则 x=10，然后解方程求出x即可得到BC的长．