题目内容
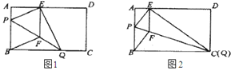
【题目】如图![]() ,在矩形纸片
,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动.
也随之移动.
①当点![]() 与点
与点![]() 重合时(如图
重合时(如图![]() ),求菱形
),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.
【答案】(1)见解析;(2)①菱形BFEP的边长为![]() cm,②点E在边AD上移动的最大距离为2cm.
cm,②点E在边AD上移动的最大距离为2cm.
【解析】
(1)由折叠的性质得出PB=PE,BF=EF,∠BPF=∠EPF,由平行线的性质得出∠BPF=∠EFP,证出∠EPF=∠EFP,得出EP=EF,因此BP=BF=EF=EP,即可得出结论;
(2)①由矩形的性质得出BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,由对称的性质得出CE=BC=5cm,在Rt△CDE中,由勾股定理求出DE=4cm,得出AE=AD-DE=1cm;在Rt△APE中,由勾股定理得出方程,解方程得出EP=![]() cm即可;
cm即可;
②找到E点离A最近和最远的两种情况即可求出点E在边AD上移动的最大距离.当点Q与点C重合时,点E离点A最近,由①知,此时AE=1cm;当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,即可得出答案.
解:(1)∵折叠纸片使B点落在边AD上的E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF.
又∵EF∥AB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=FE=EP,
∴四边形BFEP为菱形.
(2)①如图1,
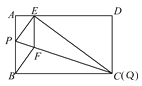
图1
∵四边形ABCD为矩形,
∴BC=AD=5cm,
CD=AB=3cm,∠A=∠D=90°.
∵点B与点E关于PQ对称,
∴CE=BC=5cm.
在Rt△CDE中,DE2=CE2-CD2,
即DE2=52-32,
∴DE=4cm,∴AE=AD-DE=5-4=1(cm).
在Rt△APE中,AE=1,AP=3-PB=3-PE,
∴EP2=12+(3-EP)2,解得EP=![]() cm,
cm,
∴菱形BFEP的边长为![]() cm.
cm.
②当点Q与点C重合时,如图1,点E离A点最近,由①知,此时AE=1cm.
当点P与点A重合时,如图2,
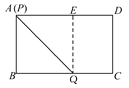
图2
点E离A点最远,此时四边形ABQE为正方形,
AE=AB=3cm,
∴点E在边AD上移动的最大距离为2cm.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】小明家2015年的四个季度的用电量情况如表1,其中各种电器用电量情况如表2.
表1 | 表2 | |||
季度名称 | 用电量/度 | 电器 | 用电量/度 | |
第一季度 | 250 | 空调 | 250 | |
第二季度 | 150 | 冰箱 | 400 | |
第三季度 | 400 | 彩电 | 150 | |
第四季度 | 200 | 其他 | 100 | |
小明根据上面的数据制成如图所示的统计图.


根据以上三幅统计图回答下列问题:
(1)从哪幅统计图中可以看出各季度用电量变化情况?
(2)从哪幅统计图中可以看出冰箱的用电量超过总用电量的![]() ?
?
(3)从哪幅统计图中可以清楚地看出空调的用电量?