题目内容
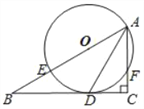
【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
【答案】(1)证明见解析;(2)![]()
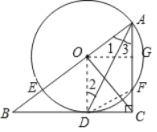
【解析】试题分析:(1)连接OD,由 OD=OA,可得∠1=∠2,再由BC为⊙O的切线,根据切线的性质可得∠ODB=90°,已知∠C=90°,所以∠ODB=∠C,即可判定OD∥AC,根据平行线的性质可得∠3=∠2,所以∠1=∠3,即可判定AD是∠BAC的平分线;(2)连接DF,已知∠B=30°,可求得∠BAC=60°,再由AD是∠BAC的平分线,可得∠3=30°,已知BC是⊙O的切线,根据弦切角定理可得∠FDC=∠3=30°,所以CD=![]() CF=
CF=![]() ,同理可得AC=
,同理可得AC=![]() CD=3,所以AF=2,过O作OG⊥AF于G,由垂径定理可得GF=
CD=3,所以AF=2,过O作OG⊥AF于G,由垂径定理可得GF=![]() AF=1,四边形ODCG是矩形,所以CG=2,OG=CD=
AF=1,四边形ODCG是矩形,所以CG=2,OG=CD=![]() ,由勾股定理可得OC=
,由勾股定理可得OC=![]() .
.
试题解析:
(1)证明:连接OD,∴OD=OA,∴∠1=∠2,
∵BC为⊙O的切线,∴∠ODB=90°,∵∠C=90°,∴∠ODB=∠C,∴OD∥AC,
∴∠3=∠2,∴∠1=∠3,∴AD是∠BAC的平分线;
(2)解:连接DF,∵∠B=30°,∴∠BAC=60°,
∵AD是∠BAC的平分线,∴∠3=30°,∵BC是⊙O的切线,∴∠FDC=∠3=30°,
∴CD=![]() CF=
CF=![]() ,∴AC=
,∴AC=![]() CD=3,∴AF=2,
CD=3,∴AF=2,
过O作OG⊥AF于G,∴GF=AF=1,四边形ODCG是矩形,
∴CG=2,OG=CD=![]() ,∴OC=
,∴OC=![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目