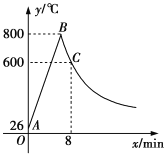
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪ![]() ĪŖÖ±½ĒĢŻŠĪ£¬
ĪŖÖ±½ĒĢŻŠĪ£¬![]() £¬
£¬![]() £¬
£¬![]() £®µć
£®µć![]() “Ó
“Ó![]() ³ö·¢ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ
³ö·¢ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ![]() ŌĖ¶Æ£»µć
ŌĖ¶Æ£»µć![]() “Ó
“Ó![]() Ķ¬Ź±³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ
Ķ¬Ź±³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ![]() ŌĖ¶Æ£®ĘäÖŠŅ»øö¶Æµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øö¶ÆµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®¹żµć
ŌĖ¶Æ£®ĘäÖŠŅ»øö¶Æµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øö¶ÆµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®¹żµć![]() ×÷
×÷![]() “¹Ö±
“¹Ö±![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ½»
½»![]() ÓŚ
ÓŚ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £®
£®
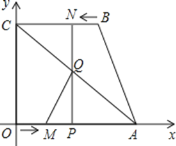
(1) Ēó![]() µÄĆ껿
µÄĆ껿![]() ÓėŌĖ¶ÆŹ±¼ä
ÓėŌĖ¶ÆŹ±¼ä![]() µÄŗÆŹż¹ŲĻµŹ½£¬ ²¢Š“³ö×Ō±äĮæ
µÄŗÆŹż¹ŲĻµŹ½£¬ ²¢Š“³ö×Ō±äĮæ![]() µÄȔֵ·¶Ī§£¬ µ±
µÄȔֵ·¶Ī§£¬ µ±![]() ĪŖŗĪÖµŹ±£¬
ĪŖŗĪÖµŹ±£¬![]() µÄÖµ×ī“ó£æ
µÄÖµ×ī“ó£æ
(2)ŹĒ·ń“ęŌŚµć![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() ĪŖÖ±½ĒČż½ĒŠĪ?Čō“ęŌŚ£¬Ēó³öµć
ĪŖÖ±½ĒČż½ĒŠĪ?Čō“ęŌŚ£¬Ēó³öµć![]() µÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
(3) µ±![]() ĪŖŅŌ
ĪŖŅŌ![]() ĪŖµ×µÄµČŃüČż½ĒŠĪŹ±£¬Ēó
ĪŖµ×µÄµČŃüČż½ĒŠĪŹ±£¬Ēó![]() Öµ£®
Öµ£®
(4) ŹĒ·ń“ęŌŚÕāŃłµÄ![]() Öµ£¬Ź¹Ö±Ļß
Öµ£¬Ź¹Ö±Ļß![]() ½«
½«![]() µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö?Čō“ęŌŚ£¬Ēó³ö
µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö?Čō“ęŌŚ£¬Ēó³ö![]() Öµ£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
Öµ£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() £¬µ±
£¬µ±![]() Ź±£¬ÓŠ
Ź±£¬ÓŠ![]() £»£Ø2£©
£»£Ø2£©![]() »ņ
»ņ![]() £»£Ø3£©
£»£Ø3£©![]() £»£Ø4£©“ęŌŚ£¬µ±
£»£Ø4£©“ęŌŚ£¬µ±![]() Ź±£¬Ö±Ļß
Ź±£¬Ö±Ļß![]() ½«
½«![]() µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö.
µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö.
”¾½āĪö”æ
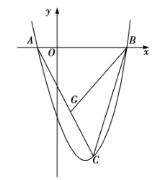
£Ø1£©¹żµćB×÷BD”ĶxÖįÓŚD£¬øł¾Ż¾ŲŠĪµÄŠŌÖŹæɵĆBN=PD=t£¬OD=BC=3£¬Č»ŗóøł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹæɵĆ![]() ,øł¾ŻČż½ĒŠĪĆ껿¹«Ź½¼“æÉĒó³ö
,øł¾ŻČż½ĒŠĪĆ껿¹«Ź½¼“æÉĒó³ö![]() µÄĆ껿
µÄĆ껿![]() ÓėŌĖ¶ÆŹ±¼ä
ÓėŌĖ¶ÆŹ±¼ä![]() µÄŗÆŹż¹ŲĻµŹ½£¬Č»ŗóøł¾ŻĢāŅā¼“æÉĒó³ötµÄȔֵ·¶Ī§£¬ŌŁĄūÓƶž“ĪŗÆŹżĒó×īÖµ¼“æÉ£»
µÄŗÆŹż¹ŲĻµŹ½£¬Č»ŗóøł¾ŻĢāŅā¼“æÉĒó³ötµÄȔֵ·¶Ī§£¬ŌŁĄūÓƶž“ĪŗÆŹżĒó×īÖµ¼“æÉ£»
£Ø2£©øł¾ŻÖ±½ĒµÄĒéæö·ÖĄąĢÖĀŪ£¬·Ö±šÕŅ³öµČĮæ¹ŲĻµĮŠ³ö·½³Ģ£¬¼“æÉĒó³ötµÄÖµ£»
£Ø3£©·Ö±šÓĆŗ¬tµÄŹ½×Ó±ķŹ¾³öAQŗĶAM£¬Č»ŗóøł¾ŻµČŃüČż½ĒŠĪµÄ¶ØŅåĮŠ·½³Ģ£¬¼“æÉĒó³ötµÄÖµ£»
£Ø4£©·Ö±šĒó³öÖ±Ļß![]() ½«
½«![]() µÄÖܳ¤Ę½·ÖµÄtÖµŗĶÖ±Ļß
µÄÖܳ¤Ę½·ÖµÄtÖµŗĶÖ±Ļß![]() ½«
½«![]() µÄĆę»żĘ½·ÖµÄtÖµ£¬Čē¹ūĮ½øötÖµĻąµČ¼““ęŌŚ£¬²»ĻąµČ¼“²»“ęŌŚ£®
µÄĆę»żĘ½·ÖµÄtÖµ£¬Čē¹ūĮ½øötÖµĻąµČ¼““ęŌŚ£¬²»ĻąµČ¼“²»“ęŌŚ£®
½ā£ŗ£Ø1£©¹żµćB×÷BD”ĶxÖįÓŚD
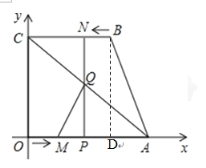
Ņ×ÖŖ£ŗĖıߊĪCOPN”¢ĖıߊĪNPDBŗĶĖıߊĪCODB¾łĪŖ¾ŲŠĪ
”ąBN=PD=t£¬OD=BC=3
![]()
”ąAD=OA£OD=1![]()
![]()
![]()
![]()
µćM“ÓµćOµ½µćAĖłŠčŹ±¼äĪŖ£ŗOA”Ā2=2s£¬µćN“ÓµćBµ½µćCĖłŠčŹ±¼äĪŖ£ŗBC”Ā1=3s£¬
”ą![]()
»ÆĪŖ¶„µćŹ½£¬µĆ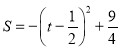 £¬ĘäÖŠ-1£¼0
£¬ĘäÖŠ-1£¼0
”ąµ±![]() Ź±£¬ÓŠ
Ź±£¬ÓŠ![]()
£Ø2£©¢Łµ±![]() Ź±£¬
Ź±£¬
![]()
”ą”÷AQMĪŖµČŃüÖ±½ĒČż½ĒŠĪ
”ßQP”ĶAM
”ąQPĪŖ”÷AQMµÄÖŠĻß
![]()
![]()
½āµĆ£ŗ![]()
¢Ś![]() Ź±£¬“ĖŹ±MÓėPÖŲŗĻ
Ź±£¬“ĖŹ±MÓėPÖŲŗĻ
”ą![]()
![]()
½āµĆ![]()
×ŪÉĻ£¬![]() »ņ
»ņ![]()
£Ø3£©”ß![]() ĪŖŅŌ
ĪŖŅŌ![]() ĪŖµ×µÄµČŃüČż½ĒŠĪ
ĪŖµ×µÄµČŃüČż½ĒŠĪ
![]()
ŌŚRt”÷AQPÖŠ![]()
ӧ![]()
”ą![]()
½āµĆ£ŗ![]()
£Ø4£©Ćę»żĘ½·ÖŹ±£¬¼“S”÷APQ=![]() S”÷AOC
S”÷AOC
![]()
¼“![]()
½āµĆ£ŗ![]() »ņ
»ņ![]() £Ø²»·ūŗĻŹµ¼Ź£¬¹ŹÉįČ„£©
£Ø²»·ūŗĻŹµ¼Ź£¬¹ŹÉįČ„£©
Öܳ¤Ę½·ÖŹ±£ŗ![]() £®
£®
¼“![]()
½āµĆ![]()
×ŪÉĻĖłŹö£ŗµ±![]() Ź±£¬Ö±Ļß
Ź±£¬Ö±Ļß![]() ½«
½«![]() µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö£®
µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö£®

 æŚĖćÄÜŹÖĻµĮŠ“š°ø
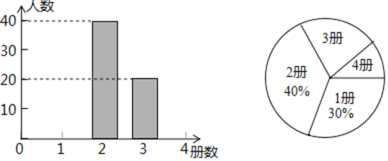
æŚĖćÄÜŹÖĻµĮŠ“š°ø”¾ĢāÄæ”æ±ķÖŠĖłĮŠ ![]() µÄ7¶ŌÖµŹĒ¶ž“ĪŗÆŹż
µÄ7¶ŌÖµŹĒ¶ž“ĪŗÆŹż![]() Ķ¼ĻóÉĻµÄµćĖł¶ŌÓ¦µÄ×ų±ź£¬ĘäÖŠ
Ķ¼ĻóÉĻµÄµćĖł¶ŌÓ¦µÄ×ų±ź£¬ĘäÖŠ ![]()
x | ” |
|
|
|
|
|
|
| ” |
y | ” | 7 | m | 14 | k | 14 | m | 7 | ” |
øł¾Ż±ķÖŠĢį¹©µÄŠÅĻ¢£¬ÓŠŅŌĻĀ4 øöÅŠ¶Ļ£ŗ
¢Ł ![]() £»¢Ś
£»¢Ś ![]() £»¢Ū µ±
£»¢Ū µ±![]() Ź±£¬y µÄÖµŹĒ k£»¢Ü
Ź±£¬y µÄÖµŹĒ k£»¢Ü ![]() ĘäÖŠÅŠ¶ĻÕżČ·µÄŹĒ £Ø £©
ĘäÖŠÅŠ¶ĻÕżČ·µÄŹĒ £Ø £©
A. ¢Ł¢Ś¢Ū B. ¢Ł¢Ś¢Ü C. ¢Ł¢Ū¢Ü D. ¢Ś¢Ū¢Ü