题目内容
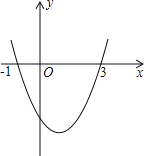
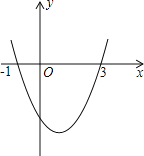
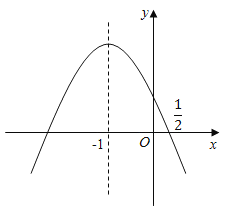
【题目】如图，已知抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
（1）若直线y＝mx+n经过B、C两点，求直线BC和抛物线的解析式；
（2）在抛物线的对称轴x＝﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标：
（3）在抛物线上存在点P(不与C重合)，使得△APB的面积与△ACB的面积相等，求点P的坐标．
【答案】（1）y＝﹣x2﹣2x+3，y＝x+3；（2）点M（﹣1，2）；（3）点P的坐标为：（﹣2，3）或（
，﹣3）或（
，﹣3）．
【解析】
（1）根据抛物线的对称性求出B（﹣3，0），然后可设交点式为y＝a（x﹣1）（x+3），代入（0，3）求出a即可；然后再根据B、C坐标利用待定系数法求直线BC的解析式即可；
（2）点A关于抛物线对称轴的对称点为点B，直线BC交抛物线对称轴于点M，则点M即为所求，据此即可得解；
（3）△APB的面积与△ACB的面积相等，则|yP|＝yC＝3，即x22x＋3＝±3，求解即可．
（1）∵抛物线经过A（1，0），且对称轴为直线x＝﹣1，
∴点B（﹣3，0），
设抛物线的表达式为：y＝a（x﹣1）（x+3），
代入C（0，3）得：3＝a×（﹣1）×3，
解得：a＝﹣1，
故抛物线的表达式为：y＝﹣（x﹣1）（x+3）＝﹣x2﹣2x+3；
由直线BC的解析式为：y＝mx+n，
代入B（﹣3，0），C（0，3）得：
，解得：
，
∴直线BC的解析式为：y＝x+3；
（2）点A关于抛物线对称轴的对称点为点B（﹣3，0），直线BC交函数对称轴于点M，则点M即为所求，
∵直线BC的解析式为：y＝x+3，
当x＝﹣1时，y＝2，
∴点M（﹣1，2）；
（3）△APB的面积与△ACB的面积相等，则|yP|＝yC＝3，
即﹣x2﹣2x+3＝±3，
当﹣x2﹣2x+3＝3时，解得：x1＝－2，x2＝0（舍去），
当﹣x2﹣2x+3＝－3时，解得：x1＝，x2＝，
故点P的坐标为：（﹣2，3）或（，﹣3）或（，﹣3）．
