题目内容
【题目】如图,直线 AB与坐标轴交与点![]() , 动点P沿路线
, 动点P沿路线![]() 运动.
运动.

(1)求直线AB的表达式;
(2)当点P在OB上,使得AP平分![]() 时,求此时点P的坐标;
时,求此时点P的坐标;
【答案】(1)y=![]() x+6;(2)P(3,0).
x+6;(2)P(3,0).
【解析】
1)直接利用待定系数法即可得出结论;
(2)方法1、利用角平分线判断出BC=AB=10,进而判断出△AOP∽△CBP,求出OP,即可得出结论;
方法2、先判断出OP=PM,设OP=m,得出PM=m,BP=8-m,再求出AM=OA=6,进而得出BM=AB-AM=4,最后用勾股定理建立方程求解即可得出结论.
解:(1)设直线AB的解析式为y=kx+b,
∵A(0,6),B(8,0),
∴![]() ,
,
∴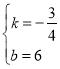 ,
,
∴直线AB的解析式为y=![]() x+6;
x+6;
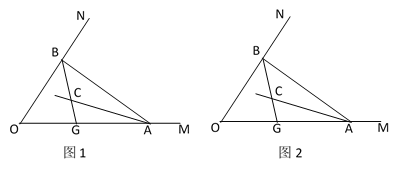
(2)方法1、如图1,
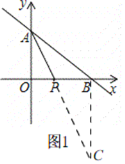
∵A(0,6),B(8,0),
∴OA=6,OB=8,AB=10,
过点B作BC∥OA交AP的延长线于C,
∴∠C=∠OAP,
∵AP平分∠OAB,
∴∠OAP=∠BAP,
∴∠C=∠BAP,
∴BC=AB=10,
∵BC∥OA,
∴△AOP∽△CBP,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴OP=3,
∴P(3,0);
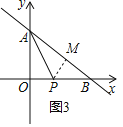
方法2、如图3,过点P作PM⊥AB于M,
∵AP是∠OAB的角平分线,
∴OP=PM,
设OP=m,
∴PM=m,
∴BP=OB-OP=8-m
易知,△AOP≌△AMP,
∴AM=OA=6,
∴BM=AB-AM=4,
在Rt△BMP中,根据勾股定理得,m2+16=(8-m)2,
∴m=3,
∴P(3,0).
故答案为:(1)y=![]() x+6;(2)P(3,0).
x+6;(2)P(3,0).

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目