题目内容
【题目】如图，在小正方形的边长均为1的方格纸中，有线段AB，点A、B均在小正方形的顶点上
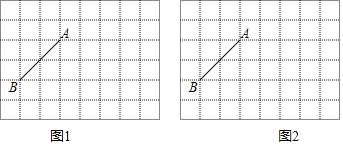
（1）在图1中画一个以线段AB为一边的矩形，点C、D均在小正方形的顶点上，且矩形ABCD的面积为4；
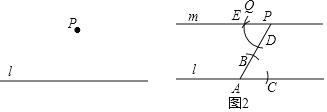
（2）在图2中画一个三角形△ABE，点E在小正方形的顶点上，且△ABE的面积为2，且∠AEB的正切值为
，请直接写出BE的长．
【答案】（1）如图所示：矩形ABCD即为所求；见解析；（2）如图所示：△AEB即为所求，见解析，BE＝2
．
【解析】
（1）直接利用网格结合矩形的性质进而分析得出答案；
（2）直接利用三角形面积求法以及正切的定义分析得出答案．
解：（1）由勾股定理可得AB=
=
，
因为矩形的面积为4，
所以矩形的另一条边长AD=4÷=
，
如图1所示：矩形ABCD即为所求；
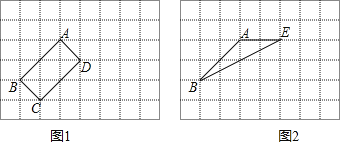
（2）如图2所示：△AEB即为所求，
BE＝
＝
．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
