题目内容
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小宇从课本上研究函数的活动中获得启发,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小宇的探究过程,请补充完整:
(1)函![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)如图,在平面直角坐标系xOy中,完成以下作图步骤:
①画出函数![]() 和
和![]() 的图象;
的图象;
②在x轴上取一点P,过点P作x轴的垂线l,分别交函数![]() 和
和![]() 的图象于点M,N,记线段MN的中点为G;
的图象于点M,N,记线段MN的中点为G;
③在x轴正半轴上多次改变点P的位置,用②的方法得到相应的点G,把这些点用平滑的曲线连接起来,得到函数![]() 在y轴右侧的图象.继续在x轴负半轴上多次改变点P的位置,重复上述操作得到该函数在y轴左侧的图象.
在y轴右侧的图象.继续在x轴负半轴上多次改变点P的位置,重复上述操作得到该函数在y轴左侧的图象.
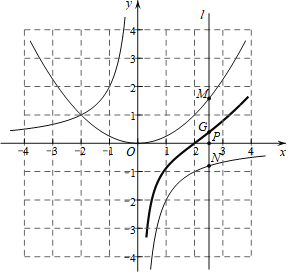
(3)结合函数![]() 的图象,发现:
的图象,发现:
①该函数图象在第二象限内存在最低点,该点的横坐标约为(保留小数点后一位);
②该函数还具有的性质为: (一条即可).
【答案】(1)x≠0;(2)详见解析;(3)当x>0时,y随x的增大而增大.
【解析】
(1)根据分式的意义,可得到结果.
(2)根据二次函数的图像性质,画出![]() 的图像,根据反比例函数的图像性质,画出
的图像,根据反比例函数的图像性质,画出![]() 的图像,在x轴上取一点P,过点P作x轴的垂线l,与两个函数图像相较于M、N两点,取出M、N中点G,然后在x轴上取不同的点P,重复做出不同的点G.得到图像.
的图像,在x轴上取一点P,过点P作x轴的垂线l,与两个函数图像相较于M、N两点,取出M、N中点G,然后在x轴上取不同的点P,重复做出不同的点G.得到图像.
(3)根据所得的函数图像,分析它的性质,写出第二象限内的最低点的坐标,得出结果.
解:(1)∵x在分母上,
∴x≠0.
故函数y=![]() 的自变量x的取值范围是x≠0;
的自变量x的取值范围是x≠0;
(2)画出该函数在y轴左侧的图象如图:
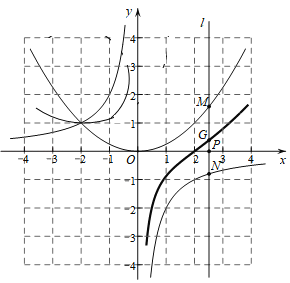
(3)①点的横坐标约为﹣1.6;(在﹣1.9至﹣1.3之间即可)
②该函数的其它性质:当x>0时,y随x的增大而增大.
故答案为:当x>0时,y随x的增大而增大.

【题目】某“兴趣小组”根据学习函数的经验,对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.

(1)函数y=x+![]() 的自变量取值范围是________;
的自变量取值范围是________;
(2)下表是x与y的几组对应值:
x | … | -3 | -2 | -1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | - | -2 | - | - |
|
| 2 |
| m | … |
则表中m的值为________;
(3)根据表中数据,在如图所示平面直角坐标xOy中描点,并画出函数的一部分,请画出
(4)观察函数图象:写出该函数的一条性质
(5)进一步探究发现:函数y=x+![]() 图象与直线y=-2只有一交点,所以方程x+
图象与直线y=-2只有一交点,所以方程x+![]() =-2只有1个实数根,若方程x+
=-2只有1个实数根,若方程x+![]() =k(x<0)有两个不相等的实数根,则k的取值范围是 ________.
=k(x<0)有两个不相等的实数根,则k的取值范围是 ________.