题目内容
【题目】如图，抛物线y＝ax2+bx+8与x轴交于A、B两点，交y轴于点C，连接BC，且点D坐标为（﹣2，4），tan∠OBC＝
．
（1）求抛物线的解析式；
（2）P为第四象限抛物线上一点，连接PC、PD，设点P的横坐标为t，△PCD的面积为S，求S与t的函数关系式；
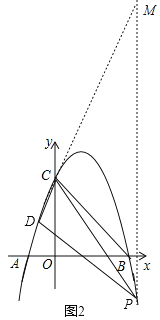
（3）延长CD交x轴于点E，连接PE，直线DG与x轴交于点G，与PE交于点Q，且OG＝2，点F在DQ上，∠DQE+∠BCF＝45°，若FQ＝2
，求点P的坐标．
【答案】（1）y＝﹣
x2+
x+8；（2）S＝t2+
t，（3）P（
，
）．
【解析】
（1）在Rt△OBC中，tan∠OBC＝
=
，则OB＝6，即可求解；
（2）S＝S△PMD﹣S△PMC＝
PM（xP﹣xD﹣xP）即可求解；
（3）证明FC是∠OCB角平分线，求出点V（
，0），点F（3，﹣1）、点Q（5，﹣3），即可求解．
（1）在Rt△OBC中，tan∠OBC＝=，∴OB＝6，
∴点B（6，0），
∴
，解得：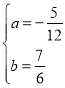
，
故抛物线的表达式为：y＝
x2+x+8…①；
（2）过点P作PM∥y轴交CD延长线于点M，
将D、C的坐标代入一次函数表达式并解得：
直线DC的表达式为：y＝2x+8，
则点E（﹣4，0），
设点M（t，2t+8），
则PM＝2t+8﹣（t2+t+8）＝t2+t，
S＝S△PMD﹣S△PMC＝PM（xP﹣xD﹣xP）＝×2（t2+t）＝t2+t，
（3）将点G（2，0）、点D坐标代入一次函数表达式并解得：
直线DG的表达式为：y＝﹣x+2…②，
∴∠DGA＝45°，
过点F作FK⊥y轴于点K，过点Q作QL⊥FK于点L交x轴于点S，直线CF交x轴于点V，
∴∠FQL＝∠LFQ＝45°，∴FL＝QL＝
FQ＝2，
设点F（m，﹣m+2），则点Q（m+2，﹣m），
tan∠FCK＝
=
，tan∠QEB＝
=，
∴∠FCK＝∠QEB，
∵∠QEB+∠BCF＝45°，∠DQE+∠QEB＝45°，
∴∠QEB＝∠BCF，∠FCK＝∠BCF，
过点V作VR⊥BC于点R，设OV＝n，
则VB＝6﹣n，CO＝CR＝8，则BR＝2，
则（6﹣n）2＝n2+4，解得：n＝，则点V（，0），
将直线C（0，8）、V（，0）坐标代入一次函数表达式并解得：
直线CV（CF）的表达式为：y＝﹣3x+8…③，
联立②③并解得：x＝3，则点F（3，﹣1），
而FQ＝2
，在等腰直角三角形FQL中，
FL＝QL＝2×＝2，
故点Q（5，﹣3），点E（﹣4，0），
同理可得直线EQ的表达式为：y＝
x﹣…④，
联立①④并解得：x＝
（舍去负值），
∴P（，）．
