��Ŀ����
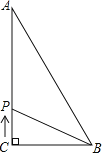
����Ŀ����ͼ����OΪԭ�㣬A��BΪ���������㣬AB=15����OA��OB=2
��1��A��B��Ӧ�����ֱ�Ϊ�� ������ ����
��2����A��B�ֱ���2����λ/���5����λ/����ٶ�������У������A��B���1����λ���ȣ�
��3����AB�ԣ�2���е��ٶ�ͬʱ�����˶�����P��ԭ��O��4����λ����ٶ������˶����Ƿ���ڳ���m��ʹ��3AP+2PB��mOPΪ��ֵ�������ڣ������mֵ�Լ������ֵ���������ڣ���˵�����ɣ�
![]()
���𰸡���10 5
��������
��1�������������OA��OB�ij���������������ʽ��
��2���ֵ�A�ڵ�B����ࡢ��A�ڵ�B���Ҳ�����������з��̽��
��3�����������г���ϵʽ�����ݶ�ֵ��ȷ���������m���ɣ�
��1����AB=15��OA��OB=2
��AO=10��BO=5
��A���Ӧ��Ϊ��10��B���Ӧ��Ϊ5
��2���辭��x���A��B���1����λ����
��|15����2+5��t|=1
��t1=2��t2=![]()
������2���![]() ��A��B���1����λ���ȣ�
��A��B���1����λ���ȣ�
��3���辭��t�룬��AP=4t������10+2t��=2t+10��PB=5+5t��4t=5+t��OP=4t
��3AP+2BP��mOP=6t+30+2t+10��m��4t=8t��4mt+40
�൱m=2ʱ��3AP+2BP��mOPΪ��ֵ����ֵΪ40��

 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�����Ŀ��������10�֣�ij���г���һ�ܼƻ�����700�����г���ƽ��ÿ���������г�100�������ڸ���ԭ��ʵ��ÿ����������ƻ�ÿ������������г��롣�±���ij�ܵ����г�������������ƻ�������Ϊ��������ƻ�������Ϊ������λ��������
���� | һ | �� | �� | �� | �� | �� | �� |
���� | ��8 | ��2 | ��3 | +16 | ��9 | +10 | ��11 |
��1�����ݼ�¼��֪ǰ���칲�������г� ����
��2����������һ��Ȳ������ٵ�һ������ ����
��3�����ó�ʵ�а����������г������Ķ��ټƹ��ʣ����Ƽ������ơ����ÿ����һ�����г��Ϳ��Ե������60 Ԫ��������������ÿ��һ���ɶ�� 15 Ԫ��������ƻ����ģ�ÿ������һ���� 15 Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ��٣�