题目内容
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)在x轴上有一点P,使得PA+PB的值最小,请求出点P的坐标.

【答案】(1)见解析;(2)P(﹣2,0).
【解析】分析:(1)根据图形旋转与平移的性质画出图形即可;
(2)作点A关于x轴的对称点A′,连接A′B交x轴于点P,利用待定系数法求出直线A′B的解析式,进而可得出P点坐标.
详解:(1)如图所示;
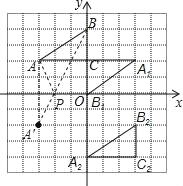
(2)作点A关于x轴的对称点A′,连接A′B交x轴于点P,则点P即为所求点,
∵A(﹣3,2),
∴A′(﹣3,﹣2).
设直线A′B的解析式为y=kx+b(k≠0),
∵A′(﹣3,﹣2),B(0,4),
∴![]() ,解得
,解得![]() ,
,
∴直线A′B的解析式为y=2x+4,
∵当y=0时,x=﹣2,
∴P(﹣2,0).

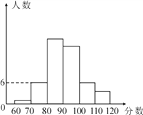
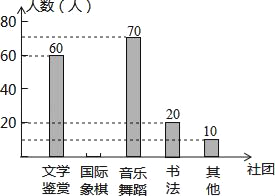
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
所占百分比 | a | 20% | b | 10% | 5% |
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
【题目】![]() 市、
市、![]() 市和
市和![]() 市分别有某种机器
市分别有某种机器![]() 台、
台、![]() 台、
台、![]() 台,现在决定把这些机器支援给
台,现在决定把这些机器支援给![]() 市
市![]() 台,
台,![]() 市
市![]() 台.己知调运机器的费用如表所示.
台.己知调运机器的费用如表所示.
|
|
| |
|
|
|
|
|
|
|
|
设从![]() 市、
市、![]() 市各调
市各调![]() 台到
台到![]() 市.
市.
(1)![]() 市调运到
市调运到![]() 市的机器为________台 (用含
市的机器为________台 (用含![]() 的式子表示);
的式子表示);
(2)![]() 市调运到
市调运到![]() 市的机器的费用为________元(用含
市的机器的费用为________元(用含![]() 的式子表示,并化简);
的式子表示,并化简);
(3)求调运完毕后的总运费(用![]() 的式子表示,并化简);
的式子表示,并化简);
(4)当![]() 和
和![]() 时,哪种调运方式总运费少?少多少?
时,哪种调运方式总运费少?少多少?