题目内容
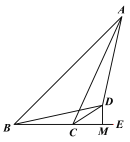
【题目】如图，等边△ABC的边长为8，AD是BC边上的中线，点E是AC边上的一点，AE=2，若点M是线段AD上的一个动点，则ME+MC的最小值为____.
【答案】
【解析】
由等边三角形的性质可知B、C关于AD对称，根据两点之间线段最短可知，连接BE，此时BE就是ME+MC的最小值.
如下图所示，连接BE，过E作EF⊥AD于F，
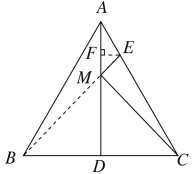
∵△ABC是等边三角形，AD是BC边上的中线，
∴AD⊥BC，
∴AD是BC的垂直平分线，
∴点C关于AD的对应点为点B，
∴BE就是EM+CM的最小值.
∵等边△ABC的边长为8，AE=2，
∴
∵EF⊥AD，AD⊥BC，
∴EF∥BC，
∴
∴
在Rt△AEF中，∠EAF=30°，AE=2，
∴EF=
AE=1， 
在Rt△ABD中，
∴DF=AD-AF=
∵
∴
在Rt△EFM中，
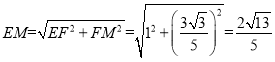
又∵
∴BE=5EM=
∴EM+CM的最小值为.
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
