题目内容
【题目】如图①,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE
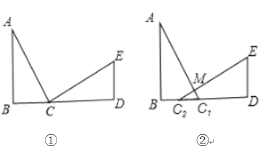
(1)求证:△ABC≌△CDE
(2)试判断AC与CE的位置关系,并说明理由.
(3)若将CD沿CB方向平移得到图②的情形,其余条件不变,此时第(2)问中AC与CE的位置关系还成立吗?请说明理由。
【答案】(1)见解析;(2)AC⊥CE ,理由见解析;(3)成立,理由见解析
【解析】
(1)利用SAS证明△ABC≌△CDE;
(2)根据△ABC≌△CDE,即可推出AC⊥CE;
(2)结论成立,根据已知推出△ABC1≌△C2DE,即可推出结论.
(1)∵AB⊥BD,ED⊥BD
∴∠ABC=∠CDE=90°
在△ABC与△CDE中
∵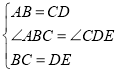
∴△ABC≌△CDE(SAS)
(2)AC⊥CE ,理由如下:
∵由(1)得:△ABC≌△CDE
∴∠A=∠DCE
∵AB⊥BD,ED⊥BD
∴∠B=∠D=90°
∴∠A+∠ACB=90°
∴∠DCE+∠ACB=90°
∴∠ACE=90°
∴AC⊥CE
(3)成立,理由如下:
∵AB⊥BD,ED⊥BD
∴∠B=∠D=90°
在△ABC1与△C2DE中
∵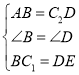
∴△ABC1≌△C2DE
∴∠A=∠EC2D
又∵∠A+∠AC1B=90°
∴∠EC2D+∠AC1B=90°
∴∠AME=90°
∴AC1⊥EC2

练习册系列答案
相关题目




