Question

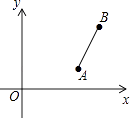
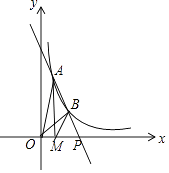
【题目】如图，一次函数y=kx+b与反比例函数y= （x＞0）的图象交于A（m，6），B（n，3）两点．
（1）求一次函数的解析式；
（2）根据图象直接写出kx+6﹣ ＞0时，x的取值范围；
（3）若M是x轴上一点，S△MOB=S△AOB ， 求点M的坐标．

Answer 1

【答案】
（1）解：把A（m，6），B（n，3）两点坐标代入y= 可得m=2，n=4，

∴A（2，6），B（4，3），

则有 ，解得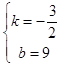

∴一次函数的解析式为y=﹣ x+9．

（2）解：观察图象可知，kx+6﹣ ＞0时，2＜x＜4．
（3）解：设直线AB交x轴于P，则P（6，0），设M（m，0），

∵S△AOB=S△OBM，

∴S△AOP﹣S△OBP=S△OBM，

∴ ×6×6﹣ ×6×3= |m|3，

解得m=±6，

∴点M的坐标为（6，0）或（﹣6，0）．

【解析】（1）首先求出A、B两点坐标，再利用待定系数法即可解决问题；（2）观察图象，一次函数的图象在反比例函数的图象上方，写出在便利店取值范围即可；（3）设直线AB交x轴于P，则P（6，0），设M（m，0），由S△AOB=S△OBM，可得S△AOP﹣S△OBP=S△OBM，列出方程即可解决问题；