题目内容
【题目】如图,在Rt△ABC中,∠B=90°,sin∠BAC= ![]() ,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 .
,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 . 
【答案】![]()
【解析】解:作BH⊥CD于H,如图,
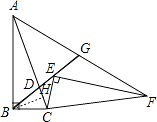
在Rt△ABC中,∠ABC=90°,∵sin∠BAC= ![]() =
= ![]() ,
,
∴AC=3BC=6,
∵BC=BD=2,
∴CH=DH,
∵∠HBC+∠ACB=90°,∠BAC+∠ACB=90°,
∴∠HBC=∠BAC,
∴sin∠HBC= ![]() ,
,
在Rt△HBC中,∵sin∠HBC= ![]() =
= ![]() ,
,
∴HC= ![]() BC=
BC= ![]() ,
,
∴CD=2CH= ![]() ,
,
∴AD=AC﹣CD=6﹣ ![]() =
= ![]() ,
,
∵Rt△ABC绕点C旋转到Rt△FEC的位置,
∴∠BCE=∠ACF,CB=CE,CA=CF,
∴∠CBE= ![]() (180°﹣∠BCE),∠CAF=
(180°﹣∠BCE),∠CAF= ![]() (180°﹣∠ACF),
(180°﹣∠ACF),
∴∠CBE=∠CAF,
∵∠BDC=∠ADG,
∴∠AGD=∠BCD,
∵BC=BD,
∴∠BCD=∠BDC,
∴∠ADG=∠AGD,
∴AG=AD= ![]() .
.
所以答案是 ![]() .
.
【考点精析】解答此题的关键在于理解余角和补角的特征的相关知识,掌握互余、互补是指两个角的数量关系,与两个角的位置无关,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
相关题目