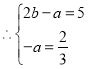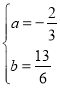题目内容
【题目】如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为 ![]() cm,AC=8cm,设运动时间为t秒.
cm,AC=8cm,设运动时间为t秒. 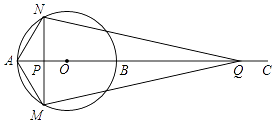
(1)求证:NQ=MQ;
(2)填空: ①当t=时,四边形AMQN为菱形;
②当t=时,NQ与⊙O相切.
【答案】
(1)证明:∵AB⊥MN,
∴PM=PN
∴AB垂直平分MN,
∴NQ=MQ;
(2)![]() ;2
;2
【解析】(2)解:①AP=t,CQ=t,则PQ=8﹣t﹣t=8﹣2t,
∵AQ⊥MN,PM=PN,
∴当AP=PQ时,四边形AMQM为菱形,
即t=8﹣2t,解得t= ![]() ;②作OH⊥QN于H,如图,
;②作OH⊥QN于H,如图,
OQ=AC﹣AO﹣CQ=8﹣ ![]() ﹣t=
﹣t= ![]() ﹣t,OP=t﹣
﹣t,OP=t﹣ ![]() ,
,
当ON⊥QN时,QN为⊙O的切线,
∵∠NOQ=∠PON,
∴△ONP∽△OQN,
∴OP:ON=ON:OQ,
即(t﹣ ![]() ):
): ![]() =
= ![]() :(
:( ![]() ﹣t),
﹣t),
整理得t2﹣8t+12=0,解得t1=2,t2=6(舍去),
∴t=2时,NQ与⊙O相切

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目