题目内容
【题目】已知数轴上的A、B、C、D四点所表示的数分别是a、b、c、d,且(a+16)2+(d+12)2=﹣|b﹣8|﹣|c﹣10|.
(1)求a、b、c、d的值;
(2)点A,B沿数轴同时出发相向匀速运动,4秒后两点相遇,点B的速度为每秒2个单位长度,求点A的运动速度;
(3)A,B两点以(2)中的速度从起始位置同时出发,向数轴正方向运动,与此同时,C点以每秒1个单位长度的速度向数轴正方向开始运动,若t秒时有2AB=CD,求t的值;
(4)A,B两点以(2)中的速度从起始位置同时出发,相向而行当A点运动到C点时,迅速以原来速度的2倍返回,到达出发点后,保持改变后的速度又折返向C点运动;当B点运动到A点的起始位置后停止运动.当B点停止运动时,A点也停止运动.求在此过程中,A,B两点同时到达的点在数轴上对应的数.
【答案】(1)a=﹣16,b=8,c=10,d=﹣12;(2)点A的运动速度为每秒4个单位长度;(3)t的值是![]() 秒或
秒或![]() 秒;(4)A,B两点同时到达的点在数轴上表示的数为:0或9或10.2.
秒;(4)A,B两点同时到达的点在数轴上表示的数为:0或9或10.2.
【解析】
(1)根据平方和绝对值的非负性即可求出结论;
(2)设点A的运动速度为每秒v个单位长度,根据题意,列出一元一次方程即可求出结论;
(3)根据题意,画出对称轴,然后用t表示点A、B、C表示的数,最后分类讨论列出方程即可求出结论;
(4)求出B点运动至A点所需的时间,然后根据点A和点B相遇的情况分类讨论,列出方程求出t的值即可求出结论.
(1)∵(a+16)2+(d+12)2=﹣|b﹣8|﹣|c﹣10|,
(a+16)2+(d+12)2+|b﹣8|+|c﹣10|=0,
∴a=﹣16,b=8,c=10,d=﹣12;
(2)设点A的运动速度为每秒v个单位长度,
4v+4×2=8+16,
v=4,
答:点A的运动速度为每秒4个单位长度;
(3)如图1,
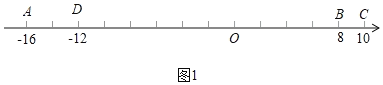
t秒时,点A表示的数为:﹣16+4t,
点B表示的数为:8+2t,
点C表示的数为:10+t.
∵2AB=CD,
①2[(﹣16+4t)﹣(8+2t)]=10+t+12,
2(﹣24+2t)=22+t,
﹣48+4t=22+t,
3t=70,
t![]() ;
;
②2[(8+2t)﹣(﹣16+4t)]=10+t+12,
2(24﹣2t)=22+t,
5t=26,
t![]() ,
,
综上,t的值是![]() 秒或
秒或![]() 秒;
秒;
(4)B点运动至A点所需的时间为![]() 12(s),故t≤12,
12(s),故t≤12,
①由(2)得:
当t=4时,A,B两点同时到达的点表示的数是﹣16+4×4=0;
②当点A从点C返回出发点时,若与B相遇,
由题意得:![]() 6.5(s),
6.5(s),![]() 3.25(s),
3.25(s),
∴点A到C,从点C返回到出发点A,用时6.5+3.25=9.75(s),
则2×4×(t﹣6.5)=10﹣8+2t,
t=9<9.75,
此时A,B两点同时到达的点表示的数是8﹣9×2=﹣10;
③当点A第二次从出发点返回点C时,若与点B相遇,则
8(t﹣9.75)+2t=16+8,
解得:t=10.2;
综上所述:A,B两点同时到达的点在数轴上表示的数为:0或9或10.2.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案