题目内容
如图在平面直角坐标系xOy中,函数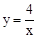 (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
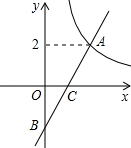
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
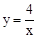 (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
解:(1)将A(m,2)代入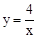 (x>0)得,m=2,
(x>0)得,m=2,
∴A点坐标为A(2,2)。
将A(2,2)代入y=kx﹣k得,2k﹣k=2,解得k=2。
∴一次函数解析式为y=2x﹣2。
(2)P点坐标为(3,0),(﹣1,0)。
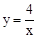 (x>0)得,m=2,
(x>0)得,m=2,∴A点坐标为A(2,2)。
将A(2,2)代入y=kx﹣k得,2k﹣k=2,解得k=2。
∴一次函数解析式为y=2x﹣2。
(2)P点坐标为(3,0),(﹣1,0)。
(1)将A点坐标代入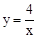 (x>0),求出m的值为2,再将(2,2)代入y=kx﹣k,求出k的值,即可得到一次函数的解析式。
(x>0),求出m的值为2,再将(2,2)代入y=kx﹣k,求出k的值,即可得到一次函数的解析式。
(2)将三角形以x轴为分界线,分为两个三角形计算,再把它们相加。
∵一次函数y=2x﹣2与x轴的交点为C(1,0),与y轴的交点为(0,﹣2),
∴S△ABP=S△ACP+S△BPC,即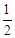 ×2CP+
×2CP+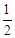 ×2CP=4,解得CP=2。
×2CP=4,解得CP=2。
∴P点坐标为(3,0),(﹣1,0)。
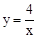 (x>0),求出m的值为2,再将(2,2)代入y=kx﹣k,求出k的值,即可得到一次函数的解析式。
(x>0),求出m的值为2,再将(2,2)代入y=kx﹣k,求出k的值,即可得到一次函数的解析式。(2)将三角形以x轴为分界线,分为两个三角形计算,再把它们相加。
∵一次函数y=2x﹣2与x轴的交点为C(1,0),与y轴的交点为(0,﹣2),
∴S△ABP=S△ACP+S△BPC,即
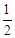 ×2CP+
×2CP+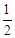 ×2CP=4,解得CP=2。
×2CP=4,解得CP=2。∴P点坐标为(3,0),(﹣1,0)。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
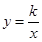 的图象过点(﹣2,1),则一次函数
的图象过点(﹣2,1),则一次函数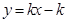 的图象不过第 象限.
的图象不过第 象限.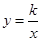 的图象经过点
的图象经过点
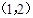 ,则
,则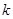 的值为( )
的值为( )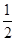
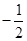
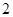
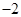
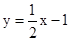 经过点C交x轴于点E,双曲线
经过点C交x轴于点E,双曲线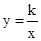 经过点D,则k的值为 .
经过点D,则k的值为 .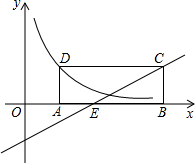
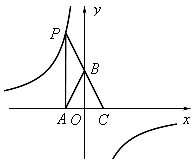
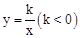 图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=
图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=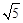 。
。
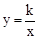 的图象经过点(5,﹣1).则实数k的值是
的图象经过点(5,﹣1).则实数k的值是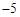
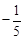
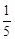
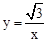 在第一象限内的图象经过OB边的中点C,则点B的坐标是
在第一象限内的图象经过OB边的中点C,则点B的坐标是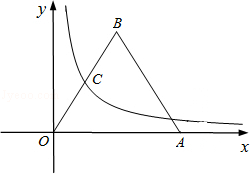
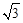 ) B.(
) B.(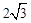 ) D,(
) D,(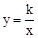 的图象经过点A(1,2),则k= .
的图象经过点A(1,2),则k= . 的图象经过点(2,4),则k的值为 .
的图象经过点(2,4),则k的值为 .