Question

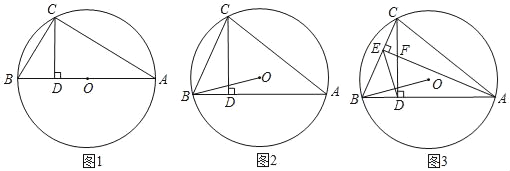
【题目】如图所示，内接于圆O，于D；

（1）如图1，当AB为直径，求证：；

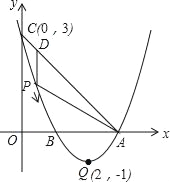
（2）如图2，当AB为非直径的弦，连接OB，则（1）的结论是否成立？若成立请证明，不成立说明由；

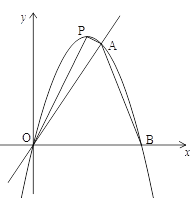
（3）如图3，在（2）的条件下，作于E，交CD于点F，连接ED，且，若，，求CF的长度．

Answer 1

【答案】（1）见解析；（2）成立；（3）

【解析】

（1）根据圆周角定理求出∠ACB=90°，求出∠ADC=90°，再根据三角形内角和定理求出即可；

（2）根据圆周角定理求出∠BOC=2∠A，求出∠OBC=90°-∠A和∠ACD=90°-∠A即可；

（3）分别延长AE、CD交⊙O于H、K，连接HK、CH、AK，在AD上取DG=BD，延长CG交AK于M，延长KO交⊙O于N，连接CN、AN，求出关于a的方程，再求出a即可．

（1）证明：∵AB为直径，

∴，

∵于D，

∴，

∴，，

∴；

（2）成立，

证明：连接OC，

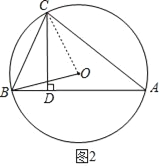
由圆周角定理得：，

∵，

∴，

∵，

∴，

∴；

（3）分别延长AE、CD交⊙O于H、K，连接HK、CH、AK，

∵，，

∴，

∴，，

∵，

∴，

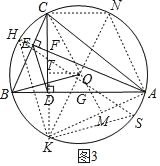
∵根据圆周角定理得：，

∴，

∴由三角形内角和定理得：，

∴，

∴，

同理，

∵，

∴，

在AD上取，延长CG交AK于M，则，

，

∴，

∴，

延长KO交⊙O于N，连接CN、AN，

则，

∴，

∵，

∴，

∴四边形CGAN是平行四边形，

∴，

作于T，

则T为CK的中点，

∵O为KN的中点，

∴，

∵，，

∴由勾股定理得：，

∴，

作直径HS，连接KS，

∵，，

∴由勾股定理得：，

∴，

∴，

设，，

∴，，

∵，

∴，

解得：，

∴，

∴．