题目内容
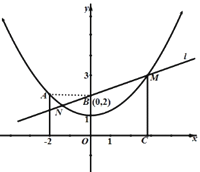
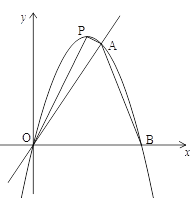
【题目】如图,抛物线y=ax2+bx的顶点为P(2,4),直线y=![]() x与抛物线交于点A.抛物线与x轴的另一个交点是点B.
x与抛物线交于点A.抛物线与x轴的另一个交点是点B.
(1)求抛物线的解析式和点A的坐标;
(2)求四边形APOB的面积;
(3)M是抛物线上位于直线y=![]() x上方的一点,当点M的坐标为多少时,△MOA的面积最大?
x上方的一点,当点M的坐标为多少时,△MOA的面积最大?
【答案】(1)y=-x2+4x,A(![]() ,
,![]() );(2)
);(2)![]() ;(3)M(
;(3)M(![]() ,
,![]() ).
).
【解析】
(1)因为顶点为P(2,4),所以带入顶点坐标公式就可以求得解析式;抛物线的解析式和直线解析式联立组成方程组,即可求出点A的坐标;
(2)把四边形APOB的面积分割成两个直角三角形和直角梯形;
(3)作MN∥y轴,交OA于点N,设M(m,-m2+4m),则N(m,![]() m),所以MN=-m2+4m-
m),所以MN=-m2+4m-![]() m=-m2+
m=-m2+![]() m,可得:S△MOA=
m,可得:S△MOA=![]() ×
×![]() ×(-m2+
×(-m2+![]() m)=-
m)=-![]() m2+
m2+![]() m,根据抛物线开口向下,所以面积有最大值得解.
m,根据抛物线开口向下,所以面积有最大值得解.
解:(1)由题意得: ,解得
,解得![]()
∴y=-x2+4x
∵直线y=![]() x与抛物线交于点A ,
x与抛物线交于点A ,
∴ 解得
解得![]() ,
, ,即A(
,即A(![]() ,
,![]() )
)
(2)∵y=-x2+4x与x轴的另一个交点是点B.
∴y=0代入解析式得:-x2+4x=0,
解得x1=0 , x2=4,∴点B的坐标是(4,0)
∴S四边形APOB=![]() ×2×4+
×2×4+![]() (4+
(4+![]() )×(
)×(![]() -2)+
-2)+![]() ×(4-
×(4-![]() )×
)×![]() =
=![]()
(3)如图,作MN∥y轴,交OA于点N,设M(m,-m2+4m),则N(m,![]() m)
m)
∴MN=-m2+4m-![]() m=-m2+
m=-m2+![]() m
m
∴S△MOA=![]() ×
×![]() ×(-m2+
×(-m2+![]() m)=-
m)=-![]() m2+
m2+![]() m.
m.
∵-![]() <0,开口向下,
<0,开口向下,
∴当m= -![]() =
= ![]() 时,S△MOA最大,
时,S△MOA最大,
即M(![]() ,
,![]() )
)


练习册系列答案
相关题目