题目内容
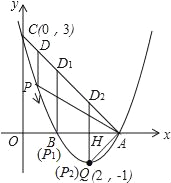
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
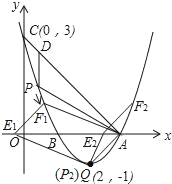
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
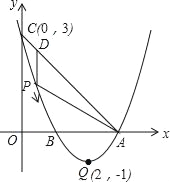
【答案】(1) y=x2﹣4x+3;(2) P1(1,0),P2(2,﹣1);(3) F1(2﹣![]() ,1),F2(2+
,1),F2(2+![]() ,1).
,1).
【解析】试题分析:(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点式,然后将函数图象经过的C点坐标代入上式中,即可求出抛物线的解析式;
(2)由于PD∥y轴,所以∠ADP≠90°,若△ADP是直角三角形,可考虑两种情况:
①以点P为直角顶点,此时AP⊥DP,此时P点位于x轴上(即与B点重合),由此可求出P点的坐标;
②以点A为直角顶点,易知OA=OC,则∠OAC=45°,所以OA平分∠CAP,那么此时D、P关于x轴对称,可求出直线AC的解析式,然后设D、P的横坐标,根据抛物线和直线AC的解析式表示出D、P的纵坐标,由于两点关于x轴对称,则纵坐标互为相反数,可据此求出P点的坐标;
(3)很显然当P、B重合时,不能构成以A、P、E、F为顶点的四边形,因为点P、F都在抛物线上,且点P为抛物线的顶点,所以PF与x轴不平行,所以只有(2)②的一种情况符合题意,由②知此时P、Q重合;假设存在符合条件的平行四边形,那么根据平行四边形的性质知:P、F的纵坐标互为相反数,可据此求出F点的纵坐标,代入抛物线的解析式中即可求出F点的坐标.
试题解析:(1)∵抛物线的顶点为Q(2,﹣1),
∴设抛物线的解析式为y=a(x﹣2)2﹣1,
将C(0,3)代入上式,得:
3=a(0﹣2)2﹣1,a=1;
∴y=(x﹣2)2﹣1,即y=x2﹣4x+3;
(2)分两种情况:
①当点P1为直角顶点时,点P1与点B重合;
令y=0,得x2﹣4x+3=0,解得x1=1,x2=3;
∵点A在点B的右边,
∴B(1,0),A(3,0);
∴P1(1,0);
②当点A为△AP2D2的直角顶点时;
∵OA=OC,∠AOC=90°,
∴∠OAD2=45°;
当∠D2AP2=90°时,∠OAP2=45°,
∴AO平分∠D2AP2;
又∵P2D2∥y轴,
∴P2D2⊥AO,
∴P2、D2关于x轴对称;
设直线AC的函数关系式为y=kx+b(k≠0).
将A(3,0),C(0,3)代入上式得:
![]() ,
,
解得![]() ;
;
∴y=﹣x+3;
设D2(x,﹣x+3),P2(x,x2﹣4x+3),
则有:(﹣x+3)+(x2﹣4x+3)=0,
即x2﹣5x+6=0;
解得x1=2,x2=3(舍去);
∴当x=2时,y=x2﹣4x+3=22﹣4×2+3=﹣1;
∴P2的坐标为P2(2,﹣1)(即为抛物线顶点).
∴P点坐标为P1(1,0),P2(2,﹣1);
(3)由(2)知,当P点的坐标为P1(1,0)时,不能构成平行四边形;
当点P的坐标为P2(2,﹣1)(即顶点Q)时,
平移直线AP交x轴于点E,交抛物线于F;
∵P(2,﹣1),
∴可设F(x,1);
∴x2﹣4x+3=1,
解得x1=2﹣![]() ,x2=2+
,x2=2+![]() ;
;
∴符合条件的F点有两个,
即F1(2﹣![]() ,1),F2(2+
,1),F2(2+![]() ,1).
,1).

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从C市运往B市的救灾物资为x吨.
(1)请填写下表;
A | B | 合计(吨) | |
C |
| x | 240 |
D |
|
| 260 |
总计(吨) | 200 | 300 | 500 |
(2)设C、D两市的总运费为W元,求W与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从C市到B市的路况得到了改善,缩短了运输时间,运费每吨减少n元(N>0),其余路线运费不变,若C、D两市的总运费的最小值不小于10080元,求n的取值范围.