题目内容
【题目】一次函数y=(k－
)x－3k+10（k为偶数）的图象经过第一、二、三象限，与x轴、y轴分别交于A、B两点，过点B作一直线与坐标轴围成的三角形面积为2，交x轴于点C.
（1）求该一次函数的解析式；
（2）若一开口向上的抛物线经过点A、B、C三点，求此抛物线的解析式。
（3）过（2）中的A、B、C三点作△ABC，求tan∠ABC的值.
【答案】（1）
（2）
（3）
【解析】
试题分析：（1）求该一次函数y=（k-
）x-3k+10（k为偶数）的解析式，需求出k的值，根据图象经过第一、二、三象限，得到k的取值范围，确定k的值，得到一次函数的解析式为y=
x+4．
（2）求抛物线的解析式，可用待定系数法，需要求出A，B，C三点的坐标，
先根据一次函数的解析式求出A、B两点的坐标，再由S△BOC=2，求出C点坐标．
（3）要求tan∠ABC的值，根据正切函数的定义，构造一个以∠ABC为内角的直角三角形，过C作CD⊥AB于D，则tan∠ABC=
．由于已知A、B、C三点的坐标，可根据三角函数的定义分别求出DC，AD的值，再算出BD的值．
试题解析：⑴（4分）由题意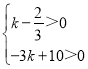得：
，解得
，又k为偶数
∴k＝2∴一次函数的解析式为
⑵（4分）求得A(－3，0)、B(0，4)，∴OB＝4
∵
＝2OC＝2，∴OC＝1
∴C(1，0)或(－1，0)
若取C(1，0)、A(－3，0)、B(0，4)，设y＝a(x＋3)(x-1)，
将B(0，4)代入，求得
，舍.
若取C(-1，0)、A(－3，0)、B(0，4)，设y＝a(x＋3)(x+1)，
将B(0，4)代入，求得
，
∴抛物线为
⑶（4分）如图，过C作CD⊥AB于D，则tan∠ABC＝
∵ Sin∠BAO＝
，cos∠BAO＝
∴ 
， DC＝
，
，AD＝
，∴BD＝
∴ tan∠ABC＝ （用相似证明也对）
