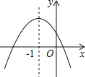题目内容
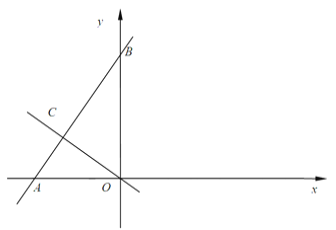
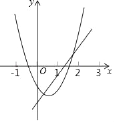
【题目】已知函数y=ax2+bx+c（a≠0）的图象与函数y=x-
的图象如图所示，则下列结论：①ab>0；②c>-；③a+b+c<-
；④方程ax2+（b-1）x+c+=0有两个不相等的实数根．其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
根据抛物线的开口方向及对称轴的位置确定a、b的符号，即可判定①；根据抛物线与y轴的交点在直线y=x﹣
与y轴交点的上方，即可判定②；观察图象可得当x=1时，ax2+bx+c＜x﹣，即可判定③；由函数y=ax2+bx+c（a≠0）的图象与函数y=x﹣的图象有两个不同的交点，即可判定④.
∵抛物线开口朝上，
∴a＞0，
∵对称轴x=﹣
在y轴的右侧，
∴b＜0，
∴ab＜0，故①错误；
∵抛物线与y轴的交点在直线y=x﹣与y轴交点的上方，
∴c＞﹣，故②正确；
观察图象可得，当x=1时，ax2+bx+c＜x﹣，即a+b+c＜﹣
；故③正确；
∵函数y=ax2+bx+c（a≠0）的图象与函数y=x﹣的图象有两个不同的交点，
∴ax2+（b﹣1）x+c+=0有两个不相等的实数根，故④正确．
故选B．
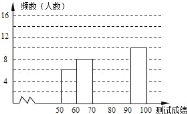
名师指导一卷通系列答案
【题目】“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
（1）①频数分布表中a的值为；②若测试成绩不低于80分为优秀，则本次测试的优秀率是；③将频数分布直方图补充完整；
（2）第5组10名同学中，有4名男同学（用A，B，C，D表示），现将这4名同学分成两组（每组2人）进行对抗练习，求A与B两名男同学能分在同一组的概率．
组别 | 成绩x分 | 频数（人数） |
第1组 | 50≤x＜60 | 6 |
第2组 | 60≤x＜70 | 8 |
第3组 | 70≤x＜80 | 14 |
第4组 | 80≤x＜90 | a |
第5组 | 90≤x＜100 | 10 |
