题目内容
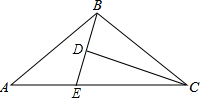 (2013•邯郸一模)如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE.若AC=5,BC=3,则BD的长为( )
(2013•邯郸一模)如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE.若AC=5,BC=3,则BD的长为( )分析:由已知条件判定△BEC的等腰三角形,且BC=CE;由等角对等边判定AE=BE,则易求BD=
BE=
AE=
(AC-BC).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:如图,∵CD平分∠ACB,BE⊥CD,
∴BC=CE.
又∵∠A=∠ABE,
∴AE=BE.
∴BD=
BE=
AE=
(AC-BC).
∵AC=5,BC=3,
∴BD=
(5-3)=1.
故选D.
∴BC=CE.
又∵∠A=∠ABE,
∴AE=BE.
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AC=5,BC=3,
∴BD=
| 1 |
| 2 |
故选D.
点评:本题考查了等腰三角形的判定与性质.注意等腰三角形“三合一”性质的运用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
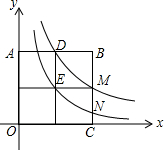 (2013•邯郸一模)如图,在直角坐标系中,正方形OABC是由四个边长为1的小正方形组成的,反比例函数
(2013•邯郸一模)如图,在直角坐标系中,正方形OABC是由四个边长为1的小正方形组成的,反比例函数