Question

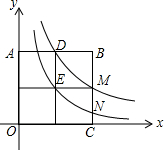（2013•邯郸一模）如图，在直角坐标系中，正方形OABC是由四个边长为1的小正方形组成的，反比例函数y1=

k1

x

(x＞0)过正方形OABC的中心E，反比例函数y2=

k2

x

(x＞0)过AB的中点D，两个函数分别交BC于点N，M，有下列四个结论：
①双曲线y₁的解析式为y1=

1

x

(x＞0)；
②两个函数图象在第一象限内一定会有交点；
③MC=2NC；
④反比例函数y₂的图象可以是看成是由反比例函数y₁的图象向上平移一个单位得到
其中正确的结论是（　　）

A．①②

B．①③

C．②④

D．③④

Answer 1

分析：首先利用待定系数法求得y1与y2的解析式，根据y1=y2的解的情况判断两个函数图象在第一象限内是否有交点，根据平移的法则即可对D进行判断．

解答：解：A、点E的坐标是（1，1），代入y₁=

k

x

，解得：k=1，则双曲线y₁的解析式为y1=

1

x

(x＞0)，命题正确；
B、点D的坐标是（1，2），代入y₂=

k2

x

得：k₂=2，则解析式是：y₂=

2

x

，方程

1

x

=

2

x

无解，故两个函数图象在第一象限内一定不会有交点，故命题错误；
C、在y₁=

1

x

中，令x=2，解得：y=

1

2

，即NC=

1

2

在y₂=

2

x

中，令x=2，解得：y=1，则MC=1，故MC=2NC正确；
D、反比例函数y₁的图象向上平移一个单位长度得到的函数的解析式是：y=

1

x

+1，故命题错误．
故选B．

点评：本题考查待定系数法求反比例函数的解析式，以及点的坐标与解析式的关系．