题目内容
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
(1)C(0,6);(2)y=- x+6;(3)P1(4,3),P2(-
x+6;(3)P1(4,3),P2(- ,
,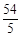 ),P3(
),P3( ,
,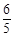 ),P4(
),P4(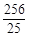 ,-
,-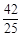 ).
).
解析试题分析:
(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
试题解析:
(1)解方程x2-14x+48=0得
x1=6,x2=8
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根
∴OC=6,OA=8
∴C(0,6)
(2)设直线MN的解析式是y=kx+b(k≠0)
由(1)知,OA=8,则A(8,0)
∵点A、C都在直线MN上
∴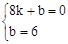
解得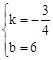 ,
,
∴直线MN的解析式为y=- x+6
x+6
(3)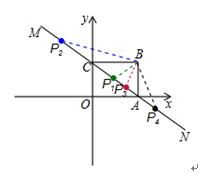
∵A(8,0),C(0,6)
∴根据题意知B(8,6)
∵点P在直线MN y=- x+6上
x+6上
∴设P(a,-- a+6)
a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(- a+6-6)2=64
a+6-6)2=64
解得,a=± ,则P2(-
,则P2(- ,
,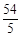 ),P3(
),P3( ,
,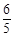 )
)
③当PB=BC时,(a-8)2+(- a+6-6)2=64
a+6-6)2=64
解得,a=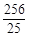 ,则-
,则- a+6=-
a+6=-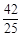
∴P4(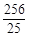 ,
,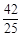 )
)
综上所述,符合条件的点P有:P1(4,3),P2(- ,
,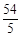 ),P3(
),P3( ,
,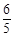 ),P4(
),P4(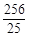 ,-
,-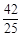 )
)
考点:一次函数综合题.

 每课必练系列答案
每课必练系列答案为提醒人们节约用水,及时修好漏水的水龙头.两名同学分别做了水龙头漏水实验,他们用于接水的量筒最大容量为100毫升.
实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升):
| 时间t(秒) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 漏出的水量V(毫升) | 2 | 5 | 8 | 11 | 14 | 17 | 20 |

(2)如果小王同学继续实验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)?
(3)按此漏水速度,一小时会漏水 千克(精确到0.1千克)
实验二:
小李同学根据自己的实验数据画出的图象如图2所示,为什么图象中会出现与横轴“平行”的部分?

 (k为常数,且
(k为常数,且 )的图象都经过点A(m,2).
)的图象都经过点A(m,2).
 满足如图的函数关系。
满足如图的函数关系。