题目内容
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称次抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点的横坐标为﹣1,求“带线”L的表达式;
(2)如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系,求m,n的值;
(3)设(2)中的“带线”L与它的“路线”l在y轴上的交点为A.已知点P为“带线”L上的点,当以点P为圆心的圆与“路线”l相切于点A时,求出点P的坐标.
【答案】(1)“带线”L的表达式为y=2x2+4x﹣4;(2)m=2,n=﹣2;(3)点P的坐标为(![]() ,
, ![]() ).
).
【解析】试题分析:
(1)由“路线l”的表达式为:y=2x-4可得,“路线l”与y轴交于点(0,-4);把x=-1代入y=2x-4可得y=-6,由此可得“带线L”的顶点坐标为(-1,-6),结合“带线L”过点(0,-4)即可求得“带线L”的解析式;
(2)由y=mx2﹣2mx+m﹣1=m(m-1)2-1可得“带线L”的顶点坐标为(1,-1),与y轴交于点(0,m-1),把这两个点的坐标代入y=nx+1即可求得m、n的值;
(3)如图,由(2)可知,若设“带线L”的顶点为B,则点B坐标为(1,﹣1),过点B作BC⊥y轴于点C,连接PA并延长交x轴于点D,由⊙P与“路线”l相切于点A可得PD⊥l于点A,由此证Rt△AOD≌Rt△BCA即可求得点D的坐标,结合点A的坐标即可求得AD的解析式为y=![]() x+1,由AD的解析式和“带线L”的解析式组成方程组,解方程组即可求得点P的坐标.
x+1,由AD的解析式和“带线L”的解析式组成方程组,解方程组即可求得点P的坐标.
试题解析:
((1)∵“带线”L的顶点横坐标是﹣1,且它的“路线”l的表达式为y=2x﹣4
∴y=2×(﹣1)﹣4=﹣6,
∴“带线”L的顶点坐标为(﹣1,﹣6).
设L的表达式为y=a(x+1)2﹣6,
∵“路线”y=2x﹣4与y轴的交点坐标为(0,﹣4)
∴“带线”L也经过点(0,﹣4),将(0,﹣4)代入L的表达式,解得a=2
∴“带线”L的表达式为 y=2(x+1)2﹣6=2x2+4x﹣4;
(2)∵直线y=nx+1与y轴的交点坐标为(0,1),
∴抛物线y=mx2﹣2mx+m﹣1与y轴的交点坐标也为(0,1),解得m=2,
∴抛物线表达式为y=2x2﹣4x+1,其顶点坐标为(1,﹣1)
∴直线y=nx+1经过点(1,﹣1),解得n=﹣2;
(3)如图,设“带线L”的顶点为B,则点B坐标为(1,﹣1),过点B作BC⊥y轴于点C,
∴∠BCA=90°,
又∵点A 坐标为(0,1),
∴AO=1,BC=1,AC=2.
∵“路线”l是经过点A、B的直线
且⊙P与“路线”l相切于点A,连接PA交 x轴于点D,
∴PA⊥AB,
∴∠DAB=∠AOD=90°,
∴∠ADO+∠DAO=90°,
又∵∠DAO+∠BAC=90°,
∴∠ADO=∠BAC,
∴Rt△AOD≌Rt△BCA,
∴OD=AC=2,
∴D点坐标为(﹣2,0)
∴经过点D、A的直线表达式为y=![]() x+1,
x+1,
∵点P为直线y=![]() x+1与抛物线L:y=2x2﹣4x+1的交点,
x+1与抛物线L:y=2x2﹣4x+1的交点,
解方程组: 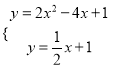 得 :
得 : ![]() (即点A舍去),
(即点A舍去),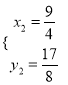 ,
,
∴点P的坐标为![]() .
.
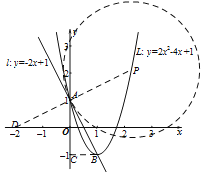

 备战中考寒假系列答案
备战中考寒假系列答案