题目内容
【题目】一副含 ![]() 和
和 ![]() 角的三角板
角的三角板 ![]() 和
和 ![]() 叠合在一起,边
叠合在一起,边 ![]() 与
与 ![]() 重合,
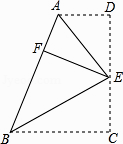
重合, ![]() (如图1),点
(如图1),点 ![]() 为边
为边 ![]()
![]() 的中点,边
的中点,边 ![]() 与
与 ![]() 相交于点
相交于点 ![]() .现将三角板
.现将三角板 ![]() 绕点
绕点 ![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 ![]() 从
从 ![]() 到
到 ![]() 的变化过程中,点
的变化过程中,点 ![]() 相应移动的路径长为 . (结果保留根号)
相应移动的路径长为 . (结果保留根号)
【答案】12 ![]() -18 cm
-18 cm
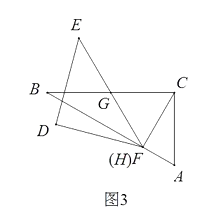
【解析】如图2和图3,在 ∠ C G F 从 0 ° 到 60 ° 的变化过程中,点H先向AB方向移,在往BA方向移,直到H与F重合(下面证明此时∠CGF=60度),此时BH的值最大,
如图3,当F与H重合时,连接CF,因为BG=CG=GF,
所以∠BFC=90度,
∵∠B=30度,
∴∠BFC=60度,
由CG=GF可得∠CGF=60度.
∵BC=12cm,所以BF=![]() BC=6
BC=6![]()
如图2,当GH⊥DF时,GH有最小值,则BH有最小值,且GF//AB,连接DG,交AB于点K,则DG⊥AB,
∵DG=FG,
∴∠DGH=45度,
则KG=KH=![]() GH=
GH=![]() ×(
×(![]() ×6
×6![]() )=3
)=3
BK=![]() KG=3
KG=3![]()
则BH=BK+KH=3![]() +3
+3
则点H运动的总路程为6![]() -(3
-(3![]() +3)+[12(
+3)+[12(![]() -1)-(3
-1)-(3![]() +3)]=12
+3)]=12![]() -18(cm)
-18(cm)
所以答案是:12![]() -18cm.
-18cm.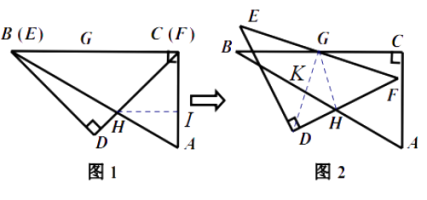
【考点精析】利用旋转的性质对题目进行判断即可得到答案,需要熟知①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目