Question

【题目】在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC=10m，拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m2）.

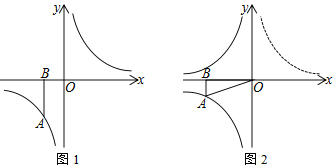
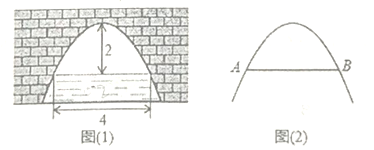
（1）如图1，若BC=4m，则S=_____m2．

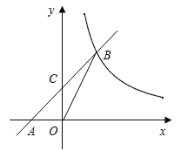
（2）如图2，现考虑在（1）中矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，则在BC的变化过程中，当S取得最小值时，边BC的长为____m．

Answer 1

【答案】88π；

【解析】

(1)小狗活动的区域面积为以B为圆心、10m为半径的圆，以C为圆心、6m为半径的圆和以A为圆心、4为半径的圆的面积和，据此列式求解可得；

(2)此时小狗活动的区域面积为以B为圆心、10为半径的圆，以A为圆心、x为半径的圆、以C为圆心、10-x为半径的圆的面积和，列出函数解析式，由二次函数的性质解答即可．

解：(1)如图，拴住小狗的10m长的绳子一端固定在B点处，小狗可以活动的区域如图所示：

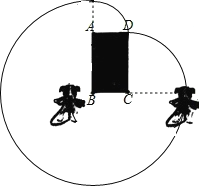
由图可知，小狗活动的区域面积为以B为圆心、10m为半径的圆，以C为圆心、6m为半径的圆和以A为圆心、4m为半径的圆的面积和，

∴S=×π102+π62+π42=88π；

（2）如图，

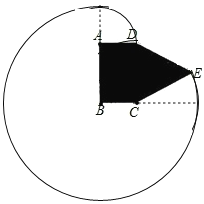
设BC=x，则AB=10-x，

∴S=π102+πx2+π(10-x)2

=(x2-5x+250)

=(x-)2+，

当x=时，S取得最小值，

∴BC=.

故答案为：(1)88π；(2).