题目内容
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).
(1)已知点A(﹣ ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线y= x+3上的一个动点,
x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标.

若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).
(1)已知点A(﹣
 ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线y=
 x+3上的一个动点,
x+3上的一个动点,①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标.

(1)①(0,2)或(0,﹣2) ②
(2)①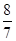 C(﹣
C(﹣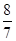 ,
, ) ②E(﹣
) ②E(﹣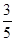 ,
, ),C(﹣
),C(﹣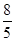 ,
, ),1
),1

(2)①
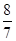 C(﹣
C(﹣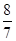 ,
, ) ②E(﹣
) ②E(﹣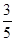 ,
, ),C(﹣
),C(﹣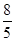 ,
, ),1
),1解:(1)①∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|﹣ ﹣0|=
﹣0|= ≠2,
≠2,
∴|0﹣y|=2,
解得,y=2或y=﹣2;
∴点B的坐标是(0,2)或(0,﹣2);
②点A与点B的“非常距离”的最小值为
(2)①如图2,

取点C与点D的“非常距离”的最小值时,需要根据运算定义“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”解答,此时|x1﹣x2|=|y1﹣y2|.即AC=AD,
∵C是直线y= x+3上的一个动点,点D的坐标是(0,1),
x+3上的一个动点,点D的坐标是(0,1),
∴设点C的坐标为(x0, x0+3),
x0+3),
∴﹣x0= x0+2,
x0+2,
此时,x0=﹣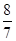 ,
,
∴点C与点D的“非常距离”的最小值为:|x0|=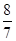 ,
,
此时C(﹣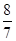 ,
, );
);
②如图3

当点E在过原点且与直线y= x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则
x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则
 ,
,
解得,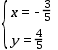 ,
,
故E(﹣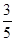 ,
, ).
).
﹣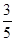 ﹣x0=
﹣x0= x0+3﹣
x0+3﹣ ,
,
解得,x0=﹣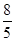 ,
,
则点C的坐标为(﹣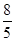 ,
, ),
),
最小值为1.
(1)①根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|0﹣y|=2,据此可以求得y的值;
②设点B的坐标为(0,y),因为|﹣ ﹣0|≥|0﹣y|,所以点A与点B的“非常距离”最小值为|﹣
﹣0|≥|0﹣y|,所以点A与点B的“非常距离”最小值为|﹣ ﹣0|=
﹣0|= ;
;
(2)①设点C的坐标为(x0, x0+3),根据材料“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”可知,C、D两点的“非常距离”的最小值为﹣x0=
x0+3),根据材料“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”可知,C、D两点的“非常距离”的最小值为﹣x0= x0+2,据此可以求得点C的坐标;
x0+2,据此可以求得点C的坐标;
②当点E在过原点且与直线y= x+3垂直的直线上时,点C与点E的“非常距离”最小,即E(﹣
x+3垂直的直线上时,点C与点E的“非常距离”最小,即E(﹣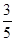 ,
, ).解答思路同上.
).解答思路同上.
∴设点B的坐标为(0,y).
∵|﹣
 ﹣0|=
﹣0|= ≠2,
≠2,∴|0﹣y|=2,
解得,y=2或y=﹣2;
∴点B的坐标是(0,2)或(0,﹣2);
②点A与点B的“非常距离”的最小值为

(2)①如图2,

取点C与点D的“非常距离”的最小值时,需要根据运算定义“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”解答,此时|x1﹣x2|=|y1﹣y2|.即AC=AD,
∵C是直线y=
 x+3上的一个动点,点D的坐标是(0,1),
x+3上的一个动点,点D的坐标是(0,1),∴设点C的坐标为(x0,
 x0+3),
x0+3),∴﹣x0=
 x0+2,
x0+2,此时,x0=﹣
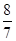 ,
,∴点C与点D的“非常距离”的最小值为:|x0|=
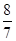 ,
,此时C(﹣
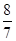 ,
, );
);②如图3

当点E在过原点且与直线y=
 x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则
x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则 ,
,解得,
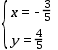 ,
,故E(﹣
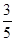 ,
, ).
).﹣
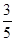 ﹣x0=
﹣x0= x0+3﹣
x0+3﹣ ,
,解得,x0=﹣
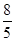 ,
,则点C的坐标为(﹣
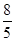 ,
, ),
),最小值为1.
(1)①根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|0﹣y|=2,据此可以求得y的值;
②设点B的坐标为(0,y),因为|﹣
 ﹣0|≥|0﹣y|,所以点A与点B的“非常距离”最小值为|﹣
﹣0|≥|0﹣y|,所以点A与点B的“非常距离”最小值为|﹣ ﹣0|=
﹣0|= ;
;(2)①设点C的坐标为(x0,
 x0+3),根据材料“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”可知,C、D两点的“非常距离”的最小值为﹣x0=
x0+3),根据材料“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”可知,C、D两点的“非常距离”的最小值为﹣x0= x0+2,据此可以求得点C的坐标;
x0+2,据此可以求得点C的坐标;②当点E在过原点且与直线y=
 x+3垂直的直线上时,点C与点E的“非常距离”最小,即E(﹣
x+3垂直的直线上时,点C与点E的“非常距离”最小,即E(﹣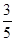 ,
, ).解答思路同上.
).解答思路同上.
练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 x+b,求n的值.
x+b,求n的值. 与x轴、y轴分别交于点A、B,点C在线段AB上,且
与x轴、y轴分别交于点A、B,点C在线段AB上,且 .
. 上时,求该抛物线的表达式;
上时,求该抛物线的表达式;
 ,
, ,
, ,…按如图所示的方式放置,点
,…按如图所示的方式放置,点 和点
和点 分别在直线
分别在直线 和
和 轴上,已知点
轴上,已知点 ,则
,则 的坐标是 .
的坐标是 . 

 ,CD=7.直线l经过A,D两点,且sin∠DAB=
,CD=7.直线l经过A,D两点,且sin∠DAB= .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
 ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;
 与坐标轴相交于A、B两点,与双曲线
与坐标轴相交于A、B两点,与双曲线 交于点C.A、D两点关于y轴对称若四边形OBCD的面积为6,求k的值.
交于点C.A、D两点关于y轴对称若四边形OBCD的面积为6,求k的值.