题目内容
已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为y=- x+b,求n的值.
x+b,求n的值.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为y=-
 x+b,求n的值.
x+b,求n的值.(1)2;(2)-1,4;(3)75.
试题分析:(1)先根据平移的规律求出y=x+b的图象沿x轴向右平移2个单位后的解析式,再将原点的坐标代入即可求解;
(2)先求出y2=kx+4图象与y轴交点,则此交点在函数y=x+b图象上,求出b=4.再求出y1=x+4与x轴的交点坐标为(-4,0),则y2=kx-4的图象经过点(4,0),即可求出k=-1;
(3)先求出y1=x+b图象与y轴的交点B,与x轴的交点A的坐标,得出AO=BO=b(b>0),则∠ABC=45°,然后在直角△AOC中利用正切函数的定义求出∠ACB=60°,再根据三角形内角和定理即可求出n的值.
(1)将y=x+b的图象沿x轴向右平移2个单位后得到y=x-2+b,
由题意,得0=0-2+b,
解得b=2.
(2)∵当x=0时,y=4,
∴y2=kx+4图象与y轴交于点(0,4).
(0,4)关于y轴对称点就是本身,
∴(0,4)在函数y=x+b图象上.
∴b=4.
∴一次函数y1=x+4,它与x轴的交点坐标为(-4,0).
∵y2=kx-4的图象与y1=x+4的图象关于y轴对称,
∴y2=kx-4的图象经过点(4,0),则0=4k+4,
∴k=-1;
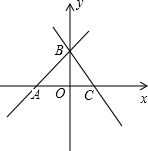
(3)∵当x=0时,y1=b,
∴y1=x+b图象与y轴交于点B(0,b).
∵当y1=0时,x=-b,
∴y1=x+b图象与x轴交于点A(-b,0).
如图,∵AO=BO=b(b>0),∴∠ABC=45°.
∵当y3=0时,x=
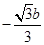 ,
,∴y3=-
 x+b图象与x轴交于点C(
x+b图象与x轴交于点C( ,0).
,0).如图,∵CO=
 ,
,∴tan∠ACB=
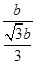 =
= ,
,∴∠ACB=60°.
∴n°=180°-∠ACB-∠ABC=75°.
即n的值为75.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
 与双曲线
与双曲线 相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC. 若△PBC的面积是20,则点C的坐标为 .
相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC. 若△PBC的面积是20,则点C的坐标为 .

 与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合),
与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合), 的值是否发生变化?( )
的值是否发生变化?( )


 ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点, x+3上的一个动点,
x+3上的一个动点,